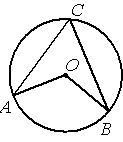
Точка О – центр окружности, /AOB=130° (см. рисунок). Найдите величину угла
ACB (в градусах).
По условию /AOB=130°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 130°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 130/2=65.
Ответ: /ACB=65°.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известно, что ∠BAC=64°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=7.
Человек, рост которого равен 1,6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина тени человека равна 2 м. Определите высоту фонаря (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: