ЕГЭ, Математика (базовый уровень). Уравнения и неравенства: Задача №620044 | Ответ-Готов

Юмор

Автор: Таська
Так выглядит современная программа обучения.
�...читать далее

ЕГЭ, Математика (базовый уровень).
Уравнения и неравенства: Задача №620044

Задача №18 из 42
Условие задачи:

Найдите корень уравнения log₃(2x-5)=2.

Решение задачи:

log₃(2x-5)=2
Так как 1=log₃3 (по второму свойству логарифмов), то уравнение можно записать в виде:
log₃(2x-5)=2log₃3
log₃(2x-5)=log₃(3²) (по шестому свойству).
log₃(2x-5)=log₃9.
Применяем потенцирование:
2x-5=9
2x=14
x=7
Ответ: 7

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №90C341

Найдите корень уравнения √2x-11=3.

Задача №455CF2

Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

НЕРАВЕНСТВА	РЕШЕНИЯ
А)	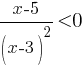1)
Б)	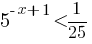2)
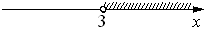
В) (x-3)(x-5)>0	3)
Г) log₂(x-3)<1	4)

В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.

Задача №0555FB

Найдите корень уравнения 9x+2(1-6x)=-x-6.

Задача №ECD5FD

Решите уравнение x²+6=5x.
Если уравнение имеет более одного корня, в ответе укажите больший из них.

Задача №ECD5FD

Решите уравнение x²+6=5x.
Если уравнение имеет более одного корня, в ответе укажите больший из них.

Комментарии:

Найти задачу

Подписаться на новости сайта

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки

X Потенцирование - решение логарифмических уравнений
Решение уравнений вида log_a(f(x))=log_a(g(x)) сводится к решению уравнения f(x)=g(x).

X

Copyright otvet-gotov.ru 2014-2021. Все права защищены.