
Задача №26 из 42 |
На координатной прямой отмечено число m и точки A, B, C и D.
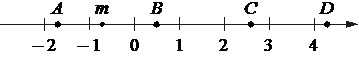
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| A | 1) √ |
| B | 2) m2 |
| C | 3) m-1 |
| D | 4) -3/m |
Заметим, что -1<m<0
Теперь будем приводить это неравенство к интересующему нас числу.
1) Приведем к √
-1<m<0 | домножим каждый член неравенства на (-1), по правилам, знак неравенства поменяется на противоположный.
-1*(-1)>m*(-1)>0*(-1)
1>-m>0 | а теперь прибавим к каждому члену 6.
1+6>-m+6>0+6
7>6-m>6 | извлечем корень из каждого члена.
√
Центральный член неравенства мы привели к интересующему нас числу, но трудно оценить значения √
√
√
3>√
Т.е. получаем, что:
3>√
Получается, что это число С.
2) Приведем к m2.
-1<m<0 | возведем каждый член в квадрат, но заметим, что m - отрицательное число, а при возведение в квадрат оно станет положительным, следовательно знак поменяется на противоположный:
(-1)2>m2>02
1>m2>0
Получается, что это число B.
3) Приведем к числу m-1.
-1<m<0 | вычтем из каждого члена 1.
-1-1<m-1<0-1
-2<m-1<-1
Очевидно, что это число A.
4) Для экономии времени на экзамене, мы не будем приводить к -3/m, а методом исключения получим, что это число D.
Ответ:
| A | 3) |
| B | 2) |
| C | 1) |
| D | 4) |
Поделитесь решением
Присоединяйтесь к нам...
Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 12 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 70 очков, если известно, что по крайней мере один раз он ошибся?
Хозяйка к празднику купила морс, мороженое, крабовые палочки и рыбу. Мороженое стоило дороже крабовых палочек, но дешевле рыбы, морс стоил дешевле мороженого. Выберите утверждения, которые верны при указанных условиях.
1) Морс стоил дешевле рыбы.
2) За морс заплатили больше, чем за мороженое.
3) Рыба — самая дорогая из покупок.
4) Среди указанных четырёх покупок есть три, стоимость которых одинакова.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решите уравнение x2+6=5x.
Если уравнение имеет более одного корня, в ответе укажите больший из них.
Виктор старше Дениса, но младше Егора. Андрей не старше Виктора. Выберите утверждения, которые верны при указанных условиях.
1) Егор самый старший из указанных четырёх человек.
2) Андрей и Егор одного возраста.
3) Виктор и Денис одного возраста.
4) Денис младше Егора.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
A) 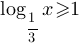
|
1) 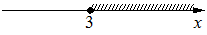
|
Б) 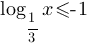
|
2) 
|
В) 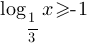
|
3) 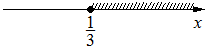
|
Г) 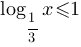
|
4) 
|
Комментарии: