
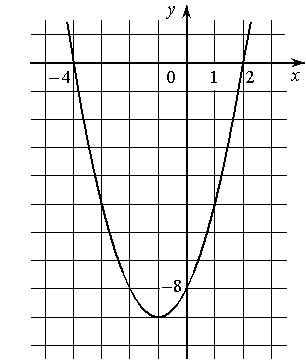
 На рисунке изображён график квадратичной функции y=ƒ(x).
На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) Функция убывает на промежутке [-1;+∞)
2) ƒ(x)>0 при x<-4 и при x>2
3) Наименьшее значение функции равно -9
Рассмотрим каждое утверждение:
1) Функция убывает на промежутке [-1;+∞).
Посмотрим по графику:
ƒ(-1)=-9
ƒ(0)=-8
ƒ(1)=-5
Т.е. ƒ(-1)<ƒ(0)<ƒ(1), следовательно на этом участке функция возрастает, следовательно, данное утверждение неверно.
2) ƒ(x)>0 при x<-4 и при x>2
По графику видно, что при x<-4 и при x>2 график располагается выше оси Х, следовательно, на данных участках ƒ(x)>0, т.е. данное утверждение верно.
3) Наименьшее значение функции равно -9.
Опять же по графику видно, что, действительно, Наименьшее значение функции равно -9 при x=-1, т.е. данное утверждение верно.
Ответ: 2) и 3)
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции 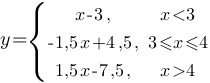 и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции 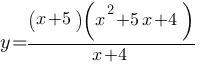 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
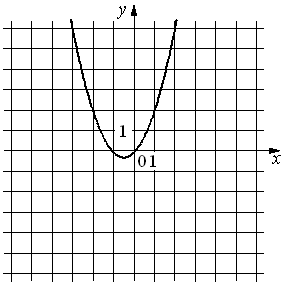 На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [-3;3] 2) [0;3] 3) [-3;-1] 4) [-3;0] |
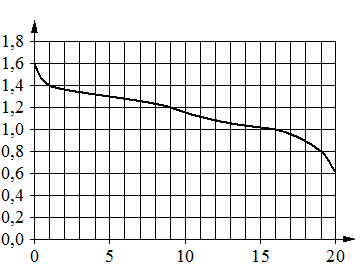 При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение за первые 16 часов работы фонарика.
При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение за первые 16 часов работы фонарика.
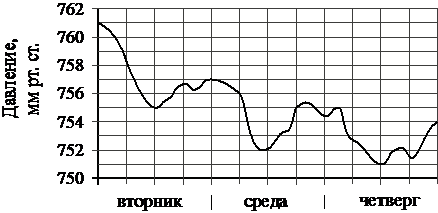 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в четверг в 12 часов дня. Ответ дайте в мм рт. ст.
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в четверг в 12 часов дня. Ответ дайте в мм рт. ст.
Комментарии: