Постройте график функции y=x2+3x-4|x+2|+2 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
В данной функции присутствуем модуль, следовательно функцию надо разложить на две функции, в зависимости от значения модуля:
|x+2|=x+2, при x+2≥0 (т.е. x≥-2)
|x+2|=-(x+2), при х+2<0 (т.е. х<-2)
Тогда вся функция будет выглядеть так:
x2+3x-4(x+2)+2, при x≥-2
x2+3x-4(-(x+2))+2, при x<-2
x2+3x-4x-8+2, при x≥-2
x2+3x-4(-x-2)+2, при x<-2
x2-x-6, при x≥-2
x2+3x+4x+8+2, при x<-2
x2-x-6, при x≥-2
x2+7x+10, при x<-2
 |
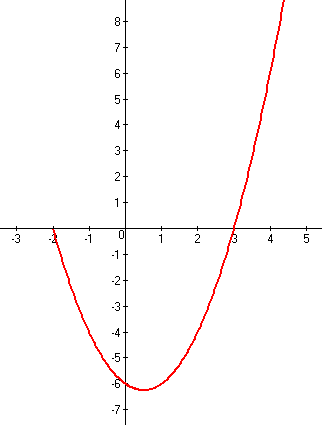График первой функции: y=x2-x-6, при x≥-2 |
 |
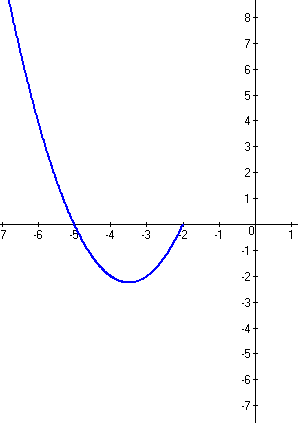График второй функции: y=x2+7x+10, при x<-2 |
 |
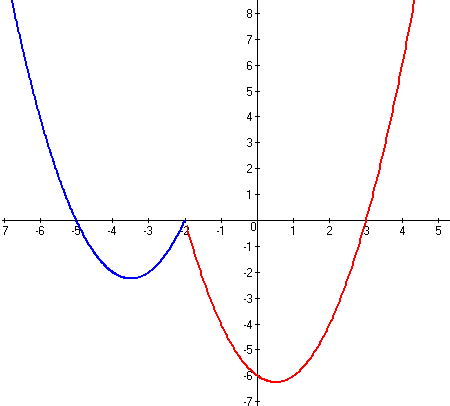Итоговый график функции y=x2+3x-4|x+2|+2 |
 |
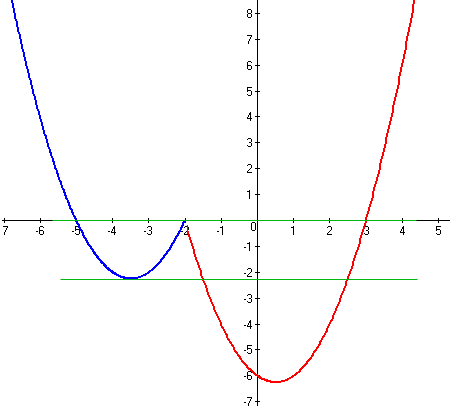Очевидно, что при m=0, функция y=m имеет ровно 3 общие точки с графиком. Но существует еще одно значение m, как показано на рисунке. Данная прямая проходит через вершину второй функции. Координату x0 вершины параболы можно найти по формуле: x0=-b/2a x0=-7/(2*1)=-3,5 Подставим в уравнение и получим, что y0=(-3,5)2+7*(-3,5)+10=12,25-24,5+10=-2,25 |
Поделитесь решением
Присоединяйтесь к нам...
Значение какого из выражений является числом иррациональным?
1) √
2) (√
3) √
4) √
Какое из данных ниже чисел является значением выражения 
?
1) 3
2) 3/13
3) 3/4
4) 3/2
Какое из данных ниже чисел является значением выражения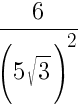 
?
1) 2/15
2) 2/25
3) 2/5
4) 2/75
Решите уравнение (x-4)(x-5)(x-6)=(x-2)(x-5)(x-6).
Какое из данных ниже чисел является значением выражения ?
1) 2/15
2) 2/25
3) 2/5
4) 2/75
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: