
Задача №28 из 42 |
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) 2x≥2 | 1) x≥1 |
| Б) 0,5x≥2 | 2) x≤1 |
| В) 0,5x≤2 | 3) x≤-1 |
| Г) 2x≤2 | 4) x≥-1 |
Чтобы решить эти неравенства надо привести их к общему основанию, т.е. чтобы и справа и слева было одно и тоже число в какой-то степени.
А) 2x≥2. Здесь все просто, слева 2 в степени х, а справа 2. Любое число - это число в первой степени. Получаем:
2x≥21
По
теореме для решения показательных неравенств:
x≥1, решение 1)
Б) 0,5x≥2. Действуем по тому же принципу, 2=0,5-1, получаем:
0,5x≥0,5-1
Так как основание меньше 1, то по
теореме для решения показательных неравенств:
x≤-1, т.е. решение 3).
В) 0,5x≤2. Аналогично пункту Б).
0,5x≤0,5-1
x≥-1, ответ 4).
Г) 2x≤2. Аналогично пункту А).
2x≤21
x≤1, ответ 2)
Ответ:
| A) | Б) | В) | Г) |
| 1) | 3) | 4) | 2) |
Поделитесь решением
Присоединяйтесь к нам...
Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 12 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 70 очков, если известно, что по крайней мере один раз он ошибся?
Виктор старше Дениса, но младше Егора. Андрей не старше Виктора. Выберите утверждения, которые верны при указанных условиях.
1) Егор самый старший из указанных четырёх человек.
2) Андрей и Егор одного возраста.
3) Виктор и Денис одного возраста.
4) Денис младше Егора.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Найдите корень уравнения 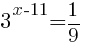
Школа приобрела стол, доску, магнитофон и принтер. Известно, что принтер дороже магнитофона, а доска дешевле магнитофона и дешевле стола. Выберите утверждения, которые верны при указанных условиях.
1) Магнитофон дешевле доски.
2) Принтер дороже доски.
3) Доска — самая дешёвая из покупок.
4) Принтер и доска стоят одинаково.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Школа приобрела стол, доску, магнитофон и принтер. Известно, что принтер дороже магнитофона, а доска дешевле магнитофона и дешевле стола. Выберите утверждения, которые верны при указанных условиях.
1) Магнитофон дешевле доски.
2) Принтер дороже доски.
3) Доска — самая дешёвая из покупок.
4) Принтер и доска стоят одинаково.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Комментарии: