Задача №33 из 42 |
Найдите корень уравнения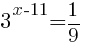 
Чтобы решить это показательное уравнение, нужно правую и левые части привести к одному основанию. Легче преобразовать правую часть, для этого избавимся от дроби с помощью отрицательной степени:
По пятому правилу работы со степенями:
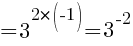
Получаем уравнение:
3x-11=3-2
Теперь воспользуемся теоремой для решения показательных уравнений:
x-11=-2
x=-2+11=9
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
Найдите корень уравнения log2(-5x+3)=-1.
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны
при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Найдите корень уравнения 9x+2(1-6x)=-x-6.
Некоторые сотрудники фирмы летом 2013 года отдыхали на даче, а некоторые — на море. Все сотрудники, которые не отдыхали на море, отдыхали на даче. Выберите утверждения, которые верны при указанных условиях.
1) Сотрудник этой фирмы, который летом 2013 года не отдыхал на даче,
не отдыхал и на море.
2) Каждый сотрудник этой фирмы отдыхал летом 2013 года или на даче,
или на море, или и там, и там.
3) Если сотрудник этой фирмы летом 2013 года не отдыхал на даче, то он отдыхал на море.
4) Если Галина летом 2013 года не отдыхала ни на даче, ни на море, то она является сотрудником этой фирмы.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Найдите корень уравнения √
Хочу получать новые решения
Ни какого спама
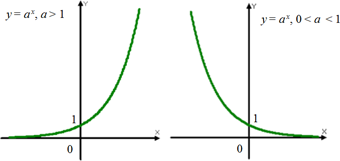
| Свойство | a>1 | 0<a<1 |
| Область определения | D(f)=(∞;+∞) | D(f)=(-∞;+∞) |
| Область значений | E(f)=(0;+∞) | E(f)=(0;+∞) |
| Монотонность | Возрастает | Убывает |
| Непрерывность | Непрерывная | Непрерывная |
Автор: Таська
Комментарии: