
Постройте график функции 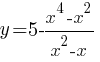 и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Область Допустимых Значений (ОДЗ):
x2-x≠0, т.к. на ноль делить нельзя.
x(x-1)≠0
x1≠0
x2≠1
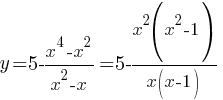

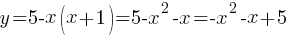
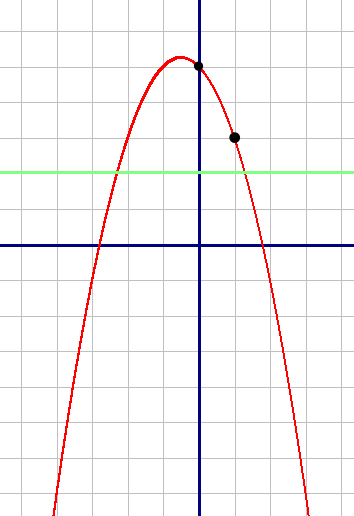 График функции - парабола, так как коэффициет "а" равен -1, т.е. меньше нуля, то ветви направлены вниз.
График функции - парабола, так как коэффициет "а" равен -1, т.е. меньше нуля, то ветви направлены вниз.| X | -2 | -1 | 0 | 1 | 2 |
| Y | 3 | 5 | 5 | 3 | -1 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=|x2-9|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
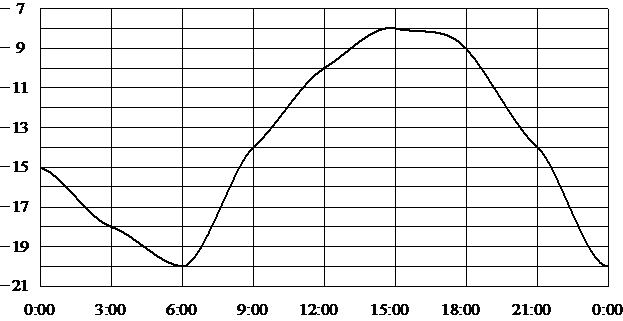 На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры во второй половине суток. Ответ дайте в градусах Цельсия.
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры во второй половине суток. Ответ дайте в градусах Цельсия.
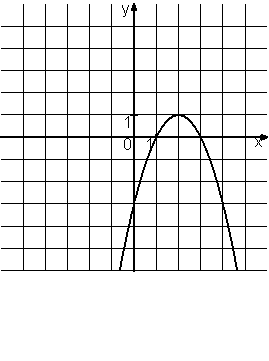 На рисунке изображена функция вида y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
На рисунке изображена функция вида y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1) [0;3]
2) [-1;1]
3) [2;4]
4) [1;4]
Постройте график функции 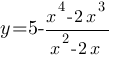 и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции y=x2-8x-4|x-3|+15 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
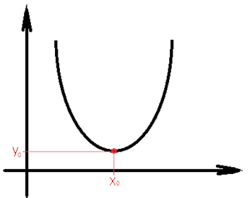 Координаты вершины параболы y=ax2+bx+c можно найти по вормулам:
Координаты вершины параболы y=ax2+bx+c можно найти по вормулам: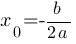
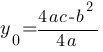
Комментарии:
(2017-03-17 02:59:14) Администратор: Людмила, спасибо большое, что заметили несоответствие. Я исправил решение.
(2017-03-16 19:24:07) Людмила: Вы выносите за скобку числителя Х^3, а числитель X^4-X^2. Наверное в условии ошибка.