
Задача №15 из 20 |
На рисунке точками показана среднесуточная температура воздуха в Москве в январе 2011 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией.
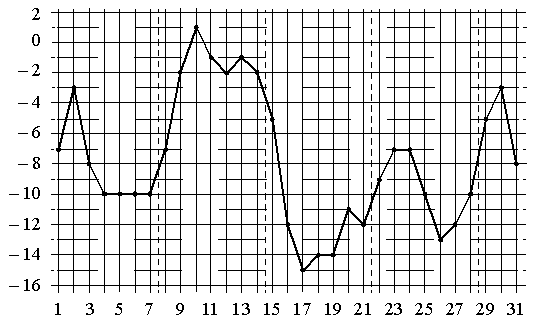
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику изменения температуры.
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 1–7 января | 1) в конце периода наблюдался рост среднесуточной температуры |
| Б) 8–14 января | 2) во второй половине периода среднесуточная температура не изменялась |
| В) 15–21 января | 3) среднесуточная температура достигла месячного минимума |
| Г) 22–28 января | 4) среднесуточная температура достигла месячного максимума |
Рассмотрим каждую характеристику:
1) в конце периода наблюдался рост среднесуточной температуры. Здесь надо внести ясность. Имеется в виду, что на последних числах периода наблюдалось повышение, а не на переходе от одного периода к другому, т.е.:
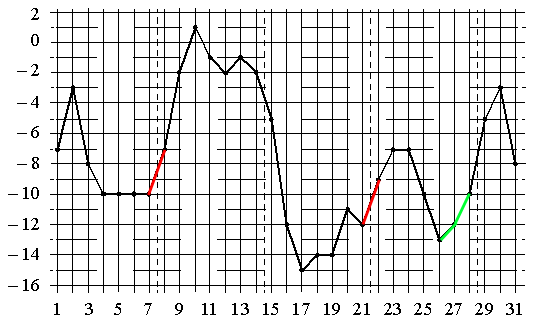
Красным цветом обозначено повышение именно при переходе от одного периода к другому, а зеленым - повышение именно в конце периода. Т.е. подходит период Г).
2) во второй половине периода среднесуточная температура не изменялась. Здесь аналогичная ситуация, учитываем неизменность температуры только в течении периода, а не при переходе:
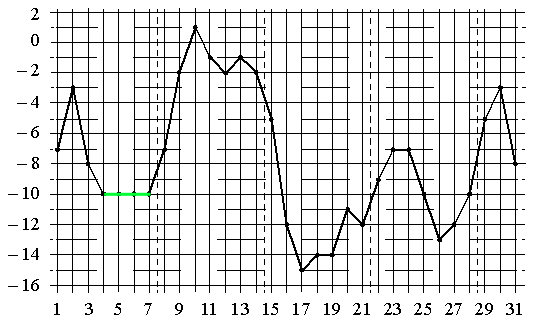
Т.е. подходит период А).
3) среднесуточная температура достигла месячного минимума. Здесь все просто, смотрим на график и находим самую низкую точку. Это 17-е число, т.е. период В).
4) среднесуточная температура достигла месячного максимума. Аналогично, самая высокая точка 10-го числа - период Б).
Ответ:
| A) | Б) | В) | Г) |
| 2) | 4) | 3) | 1) |
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображён график функции y=f(x). Числа a, b, c, d и e задают на оси Ox интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной.
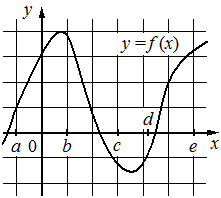
| ИНТЕРВАЛЫ | ХАРАКТЕРИСТИКИ |
| А) (a;b) | 1) значение функции положительно в каждой точке интервала |
| Б) (b;c) | 2) значение производной функции положительно в каждой точке интервала |
| В) (c;d) | 3) значение функции отрицательно в каждой точке интервала |
| Г) (d;e) | 4) значение производной функции отрицательно в каждой точке интервала |
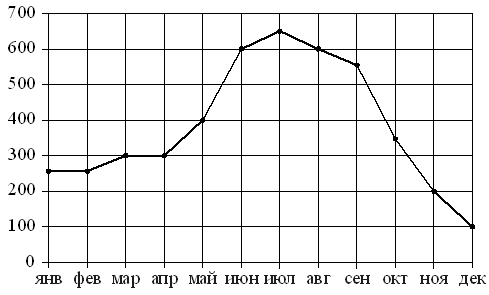
На рисунке точками показаны объёмы месячных продаж холодильников
в магазине бытовой техники. По горизонтали указываются месяцы,
по вертикали — количество проданных холодильников. Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж холодильников.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) январь-март | 1) продажи за первый и второй месяцы квартала совпадают |
| Б) апрель-июнь | 2) ежемесячный объём продаж достигает максимума за весь период |
| В) июль-сентябрь | 3) за этот период ежемесячный объём продаж увеличился на 300 холодильников |
| Г) октябрь-декабрь | 4) за последний месяц периода было продано меньше 200 холодильников |
На рисунке точками показано атмосферное давление в городе N
на протяжении трёх суток с 4 по 6 апреля 2013 года. В течение суток давление измеряется 4 раза: в 00:00, в 06:00, в 12:00 и в 18:00.
По горизонтали указывается время суток и дата, по вертикали — давление
в миллиметрах ртутного столба. Для наглядности точки соединены линией.
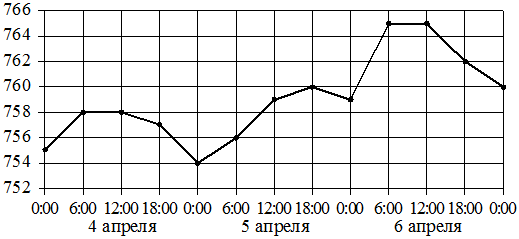
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику атмосферного давления в городе N
в течение этого периода.
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) утро 4 апреля (с 6 до 12 часов) | 1) давление не менялось и было выше 764 мм рт. ст. |
| Б) утро 5 апреля (с 6 до 12 часов) | 2) давление росло |
| В) утро 6 апреля (с 6 до 12 часов) | 3) давление не менялось и было ниже 760 мм рт. ст. |
| Г) день 6 апреля (с 12 до 18 часов) | 4) давление падало |
На рисунке точками показаны объёмы месячных продаж холодильников
в магазине бытовой техники. По горизонтали указываются месяцы,
по вертикали — количество проданных холодильников. Для наглядности точки соединены линией.
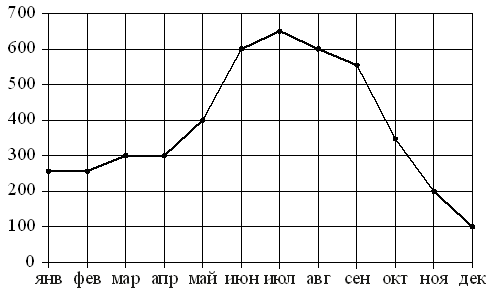
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж холодильников.
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) январь–март | 1) было продано меньше всего холодильников |
| Б) апрель–июнь | 2) ежемесячный объём продаж рос в течение всего периода |
| В) июль–сентябрь | 3) было продано около 800 холодильников |
| Г) октябрь–декабрь | 4) объём продаж падал на одно и тоже число холодильников в месяц |
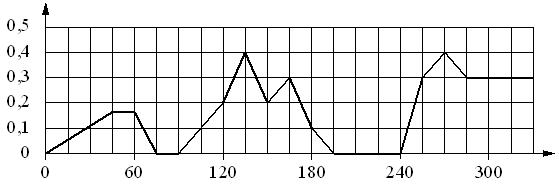 На графике изображена зависимость скорости погружения батискафа
от времени. На вертикальной оси отмечена скорость в м/с,
на горизонтальной — время в секундах, прошедшее с начала погружения.
На графике изображена зависимость скорости погружения батискафа
от времени. На вертикальной оси отмечена скорость в м/с,
на горизонтальной — время в секундах, прошедшее с начала погружения.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 60–120 c | 1) батискаф ровно 15 секунд не менял глубину |
| Б) 120–180 c | 2) скорость погружения не росла на всём интервале |
| В) 180–240 c | 3) батискаф 15 секунд погружался с постоянной ненулевой скоростью |
| Г) 240–300 c | 4) скорость погружения была не меньше 0,1 м/с на всём интервале |
Комментарии: