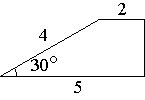
Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
Площадь
трапеции вычисляется по формуле 
, где a и b - основания трапеции,
а h - высота трапеции. Обозначим углы трапеции A, B, C и D. И проведем высоту из угла B к основанию AD, как паказано на рисунке.
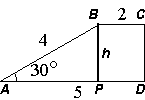Получившийся треугольник ABP -
прямоугольный c катетами BP и AP. Заметим, что BP - это катет притиволежащий углу в 30°, следовательно он равен половине
гипотенузы (
по свойству прямоугольного треугольника), h=4/2=2. Используя формулу площади трапеции получаем S=(2+5)*2/2.
Вычисляем S=7.
Ответ: S=7.
Поделитесь решением
Присоединяйтесь к нам...
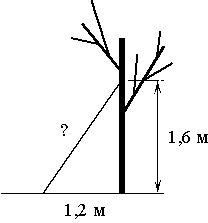Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
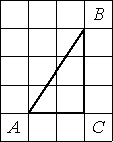Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
3) У равнобедренного треугольника есть центр симметрии.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-25 18:11:21) Lina: Огромное спасибо
(2015-05-21 18:06:36) Динар: Спасибо
(2015-05-16 09:40:34) : SPS
(2015-03-21 16:07:42) Анна: замечательно!!!!