
 На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=13. Площадь треугольника ABC равна 75. Найдите площадь треугольника ABD.
На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=13. Площадь треугольника ABC равна 75. Найдите площадь треугольника ABD.
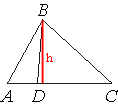 Проведем высоту из вершины B.
Проведем высоту из вершины B.
Заметим, что это высота не только треугольника ABC, но и треугольника ABD.
Найдем высоту, используя формулу площади треугольника для треугольника ABC:
SABC=AC*h/2=(AD+DC)*h/2
75=(2+13)*h/2
75=15*h/2
75*2=15h
150=15h
h=10
Теперь применим эту же формулу для треугольника ABD:
SABD=AD*h/2=2*10/2=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
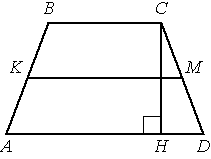 В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
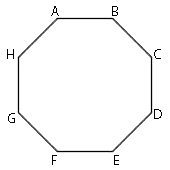 ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
 Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=122° и ∠ACB=47°. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=122° и ∠ACB=47°. Найдите угол DCB. Ответ дайте в градусах.
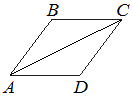 В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
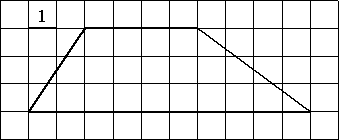 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Комментарии:
(2023-11-06 18:06:02) : дан треугольник abc на стороне ac которого взята точка d такая что ad 6 см а вс=7см отрезок дб делит треугольник абс на 2 треугольника при этом площадь треугольника абссостовляет 91кв см