
 В параллелограмме ABCD точка K — середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.
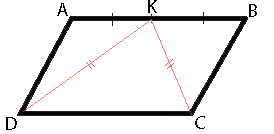
В параллелограмме ABCD точка K — середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники DAK и KBC. AK=KB, т.к. точка K - середина AB, KC=KD (из условия задачи), AD=BC (по свойству параллелограмма). Соответственно, треугольники DAK и KBC равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что /DAK=/KBC.
AD||BC (по определению параллелограмма), рассмотрим сторону AB как секущую к этим параллельным сторонам. Тогда получается, что сумма углов DAK и KBC равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.
Теперь рассмотрим стороны AB и CD, они параллельны (тоже по определению параллелограмма). Рассмотрим сторону AD как секущую к этим параллельным сторонам.
/DAK и /ADC - внутренние односторонние. Следовательно их сумма равна 180°. А так как /DAK=90°, то /ADC тоже равен 90°.
Аналогично доказывается, что /BCD тоже равен 90°.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 148°, угол ABC равен 132°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 148°, угол ABC равен 132°. Найдите угол ACB. Ответ дайте в градусах.
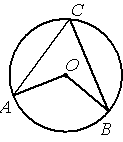 Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
 Катеты прямоугольного треугольника равны 4√
Катеты прямоугольного треугольника равны 4√
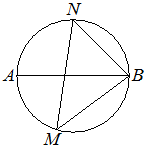 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
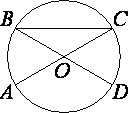 В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Комментарии:
(2016-10-09 00:43:15) Администратор: Константин, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-10-07 21:07:51) Константин: Известно, что f(x)=x^(3/2), g(x)=x^3 Докажите, что f(27x^3)=g^2(x) Докажите, что