В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
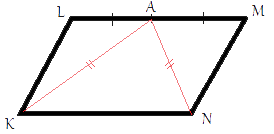Рассмотрим треугольники KLA и NMA. LA=MA, т.к. точка А - середина LM, AK=AN из условия задачи, LK=MN (по свойству параллелограмма). Соответственно, треугольники KLA и NMA равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что ∠KLA=∠NMA.
LK||MN (по определению параллелограмма), рассмотрим сторону LM как секущую к этим параллельным сторонам. Тогда получается, что сумма углов KLA и NMA равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.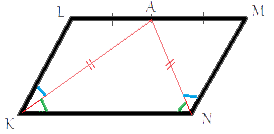
Рассмотрим треугольник KAN, KA=NA (по условию задачи), соответственно, этот треугольник
равнобедренный. Отсюда следует, что ∠AKN=∠ANK (
из свойства равнобедренного треугольника). Из ранее полученного равенства треугольников, следует, что ∠LKA=∠MNA. Получаем, что углы LKN и MNK равны.
В свою очередь они так же являются внутренними односторонними и их сумма равна 180°. Получается, что и эти углы равны 90° каждый.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 92. Найдите стороны треугольника ABC.
В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
Хорды AC и BD окружности пересекаются в точке P, BP=7, CP=14, DP=10. Найдите AP.
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-03-31 11:20:50) Администратор: Елена, а как Вы вычислили, что угол KLM прямой?
(2019-03-28 21:01:57) Елена: так как LM II KN (по определению параллелограмма), LK - секущая, то сумма односторонних углов КLM и LKM равна 180 градусам. Значит, угол LKM = 180 - 90 = 90.Угол КNМ находим аналогично.
(2017-03-29 11:10:09) Арина: Спасибо большое!!Вас сайт мне очень помогает.
(2017-03-21 20:47:45) Администратор: Евгений, да, можно и так.
(2017-03-21 08:27:03) Евгений: А нельзя после доказательства равенства углов KLA=NMA=90 сказать,что угол KLA=KNM, а угол NMA=LKN(по свойству параллелограмма) следовательно, угол KNM=LKN=90
(2015-03-21 15:41:45) Анна: прекрасно!!!!!!
(2014-11-28 02:25:10) Балобина Егор: Просто замечательно! Супер!!
(2014-05-30 15:48:44) Администратор: Мария, ну наверно, не совсем все. Здесь много подробных объяснений, которые необязательны, а даны только для понимания хода решения. Но на экзамене обязательно ссылаться на определения, теоремы, аксиомы и т.д.
(2014-05-30 15:26:18) Мария: А если на экзамене эта задача будет это все писать надо?
(2014-05-09 13:44:45) Администратор: В самом начале доказательства, выводится равенство треугольников KLA и NMA, следовательно, равны их соответствующие углы.
(2014-05-09 11:33:05) юлия:: я не поняла /KLA=/NMA.