
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
Рассмотрим каждое утверждение:
1) "Если при пересечении двух прямых третьей прямой
накрест лежащие углы равны, то прямые параллельны." Это утверждение верно,
по
свойству параллельных прямых.
2) "Диагональ
трапеции делит её на два равных треугольника." Во-первых, нет такого
свойства трапеции. 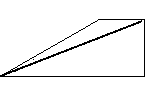 Во-вторых, если рассмотреть
прямоугольную трапецию с
проведенной диагональю, то становится очевидным, что один из получившихся треугольников -
прямоугольный, а второй - нет.
Следовательно, это утверждение неверно.
Во-вторых, если рассмотреть
прямоугольную трапецию с
проведенной диагональю, то становится очевидным, что один из получившихся треугольников -
прямоугольный, а второй - нет.
Следовательно, это утверждение неверно.
3) "Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон", это утверждение верно
(по теореме Пифагора).
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
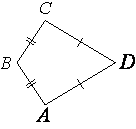 В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
 В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
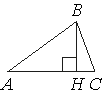 В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
Комментарии:
(2014-05-29 16:59:15) Администратор: Маша, тогда подскажите, что такое диагональ прямоугольного треугольника? )))
(2014-05-29 16:54:50) Маша: в 3 не прямоугольник должен быть написан,а прямоугольный треугольник