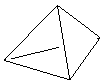
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Площадь боковой поверхности пирамиды равна сумме боковых граней пирамиды, которые являются равными треугольниками со сторонами 16, 17 и 17.
Площадь такого треугольника легче вычислить через три стороны (формула Герона).
Полупериметр:
p=(16+17+17)/2=50/2=25
S=√p(p-a)(p-b)(p-c)=√25(25-16)(25-17)(25-17)=√25*9*8*8=
По свойству арифметического корня:
=√25*√9*√8*8=5*3*8=120
Это площадь одной боковой грани, значит площадь всей боковой поверхности:
Sбп=3*S=3*120=360
Ответ: 360
Поделитесь решением
Присоединяйтесь к нам...
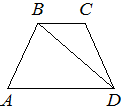В трапеции ABCD известно, что AB=CD, ∠BDA=54° и ∠BDC=23°. Найдите угол ABD. Ответ дайте в градусах.
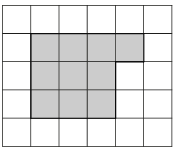План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. Ответ дайте
в квадратных метрах.
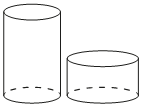Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
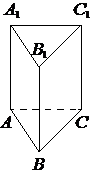Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
На координатной прямой отмечены точки A, B, C и D.
Число m равно √2.
Установите соответствие между указанными точками и числами в правом столбце, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| A | 1) 2m-5 |
| B | 2) m3 |
| C | 3) m-1 |
| D | 4) -1/m |
Хочу получать новые решения
Ни какого спама
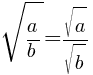, если a≥0, b≥0.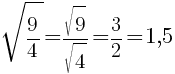
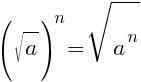, при a≥0.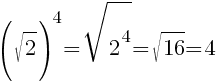
Автор: Таська
Комментарии: