Задача №12 из 42 |
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
A)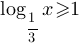 
|
1) 
|
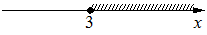
Б)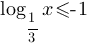 
|
2) 
|
В)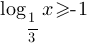 
|
3) 
|
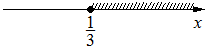
Г)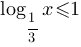 
|
4) 
|
Решим каждое неравенство:
A)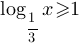
По
второму свойству логарифмов, в правой части неравенства преоразуем единицу в логарифм:
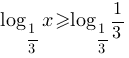
Основание логарифмоы = 1/3, т.е. меньше единицы, следовательно по
теореме для решения логарифмических неравенств:
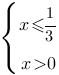
- подходит вариант 4)
Для неравенства Г)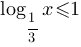 можно сразу определить ответ - вариант 3), так как неравенства отличаются только знаком.
Б)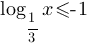
По
второму свойству логарифмов, в правой части неравенства преоразуем единицу в логарифм:
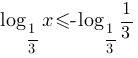
При помощи 6-го свойства, внесем -1 в логарифм.
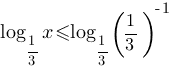
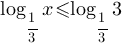
Основание логарифмоы = 1/3, т.е. меньше единицы, следовательно по
теореме для решения логарифмических неравенств:
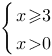
- подходит вариант 1)
Для неравенства В)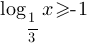 можно сразу определить ответ - вариант 2), так как неравенства отличаются только знаком.
Ответ:
| A) | Б) | В) | Г) |
| 4) | 1) | 2) | 3) |
Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) рост жирафа | 1) 6400 км |
| Б) толщина лезвия бритвы | 2) 500 см |
| В) радиус Земли | 3) 0,08 мм |
| Г) ширина футбольного поля | 4) 68 м |
Решите уравнение x2+10x+21=0.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) 2x≥2 | 1) x≥1 |
| Б) 0,5x≥2 | 2) x≤1 |
| В) 0,5x≤2 | 3) x≤-1 |
| Г) 2x≤2 | 4) x≥-1 |
Найдите корень уравнения √
Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 12 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 70 очков, если известно, что по крайней мере один раз он ошибся?
Хочу получать новые решения
Ни какого спама
Автор: Таська
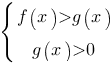
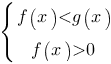
Комментарии: