
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ97 –Η–Ζ 287 |
–ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η y=-x+5|x|-x2 –Η –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö c –Ω―Ä―è–Φ–Α―è y=c –Η–Φ–Β–Β―² ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ ―Ä–Ψ–≤–Ϋ–Ψ ―²―Ä–Η –Ψ–±―â–Η–Β ―²–Ψ―΅–Κ–Η.
–£ –¥–Α–Ϋ–Ϋ–Ψ–Ι ―³―É–Ϋ–Κ―Ü–Η–Η –Ω―Ä–Η―¹―É―²―¹―²–≤―É–Β–Φ
–Φ–Ψ–¥―É–Μ―¨, ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ ―³―É–Ϋ–Κ―Ü–Η―é –Ϋ–Α–¥–Ψ ―Ä–Α–Ζ–Μ–Ψ–Ε–Η―²―¨ –Ϋ–Α –¥–≤–Β –Ω–Ψ–¥―³―É–Ϋ–Κ―Ü–Η–Η, –≤ –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―²–Η –Ψ―² –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è
–Φ–Ψ–¥―É–Μ―è:
 -x+5x-x2, –Ω―Ä–Η x≥0
-x+5x-x2, –Ω―Ä–Η x≥0
-x+5(-x)-x2, –Ω―Ä–Η x<0
 4x-x2, –Ω―Ä–Η x≥0
4x-x2, –Ω―Ä–Η x≥0
-6x-x2, –Ω―Ä–Η x<0
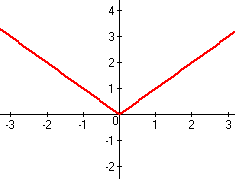
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ –Η –Ω–Ψ―¹―²―Ä–Ψ–Η–Φ –≥―Ä–Α―³–Η–Κ –¥–Μ―è –Κ–Α–Ε–¥–Ψ–Ι –Ω–Ψ–¥―³―É–Ϋ–Κ―Ü–Η–Η –Η –Ψ–±―ä–Β–¥–Η–Ϋ–Η–Φ –Η―Ö.
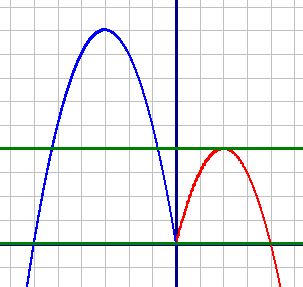 1) y1=4x-x2, –Ω―Ä–Η x≥0 (–Κ―Ä–Α―¹–Ϋ―΄–Ι –≥―Ä–Α―³–Η–Κ)
1) y1=4x-x2, –Ω―Ä–Η x≥0 (–Κ―Ä–Α―¹–Ϋ―΄–Ι –≥―Ä–Α―³–Η–Κ)
| X | 0 | 1 | 2 | 3 |
| Y | 0 | 3 | 4 | 3 |
| X | 0 | -1 | -2 | -3 | -4 |
| Y | 0 | -5 | -8 | -9 | -8 |
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
–Θ―¹―²–Α–Ϋ–Ψ–≤–Η―²–Β ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Φ–Β–Ε–¥―É –≥―Ä–Α―³–Η–Κ–Α–Φ–Η ―³―É–Ϋ–Κ―Ü–Η–Ι –Η ―³–Ψ―Ä–Φ―É–Μ–Α–Φ–Η, –Κ–Ψ―²–Ψ―Ä―΄–Β –Η―Ö –Ζ–Α–¥–Α―é―².
| –Λ–û–†–€–Θ–¦–Ϊ | –™–†–ê–Λ–‰–ö–‰ | ||
|
1) y=-3 2) y=x-3 3) y=-3x 4) y=3x |
–ê) 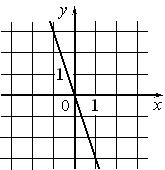 |
–ë)  |
–£)  |
–ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η y=x2-5|x|-x –Η –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö c –Ω―Ä―è–Φ–Α―è y=c –Η–Φ–Β–Β―² ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ ―Ä–Ψ–≤–Ϋ–Ψ ―²―Ä–Η –Ψ–±―â–Η–Β ―²–Ψ―΅–Κ–Η.
–ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η y=|x|x-|x|-3x –Η –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö m –Ω―Ä―è–Φ–Α―è y=m –Η–Φ–Β–Β―² ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ ―Ä–Ψ–≤–Ϋ–Ψ –¥–≤–Β –Ψ–±―â–Η–Β ―²–Ψ―΅–Κ–Η.
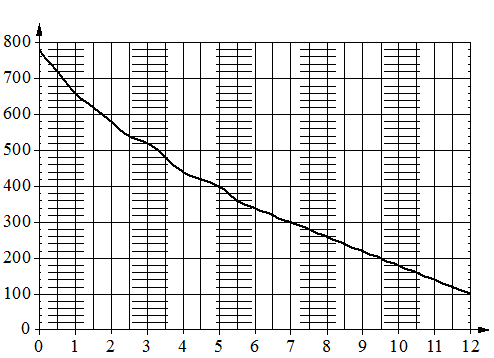 –ù–Α –≥―Ä–Α―³–Η–Κ–Β –Η–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Α –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―²―¨ –Α―²–Φ–Ψ―¹―³–Β―Ä–Ϋ–Ψ–≥–Ψ –¥–Α–≤–Μ–Β–Ϋ–Η―è –Ψ―² –≤―΄―¹–Ψ―²―΄
–Ϋ–Α–¥ ―É―Ä–Ψ–≤–Ϋ–Β–Φ –Φ–Ψ―Ä―è. –ù–Α –≥–Ψ―Ä–Η–Ζ–Ψ–Ϋ―²–Α–Μ―¨–Ϋ–Ψ–Ι –Ψ―¹–Η –Ψ―²–Φ–Β―΅–Β–Ϋ–Α –≤―΄―¹–Ψ―²–Α –Ϋ–Α–¥ ―É―Ä–Ψ–≤–Ϋ–Β–Φ –Φ–Ψ―Ä―è –≤ –Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Α―Ö, –Ϋ–Α –≤–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ–Ψ–Ι βÄî –¥–Α–≤–Μ–Β–Ϋ–Η–Β –≤ –Φ–Η–Μ–Μ–Η–Φ–Β―²―Ä–Α―Ö ―Ä―²―É―²–Ϋ–Ψ–≥–Ψ ―¹―²–Ψ–Μ–±–Α. –û–Ω―Ä–Β–¥–Β–Μ–Η―²–Β –Ω–Ψ –≥―Ä–Α―³–Η–Κ―É, –Ϋ–Α –Κ–Α–Κ–Ψ–Ι –≤―΄―¹–Ψ―²–Β –Α―²–Φ–Ψ―¹―³–Β―Ä–Ϋ–Ψ–Β –¥–Α–≤–Μ–Β–Ϋ–Η–Β ―Ä–Α–≤–Ϋ–Ψ 280 –Φ–Η–Μ–Μ–Η–Φ–Β―²―Ä–Α–Φ ―Ä―²―É―²–Ϋ–Ψ–≥–Ψ ―¹―²–Ψ–Μ–±–Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Α―Ö.
–ù–Α –≥―Ä–Α―³–Η–Κ–Β –Η–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Α –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―²―¨ –Α―²–Φ–Ψ―¹―³–Β―Ä–Ϋ–Ψ–≥–Ψ –¥–Α–≤–Μ–Β–Ϋ–Η―è –Ψ―² –≤―΄―¹–Ψ―²―΄
–Ϋ–Α–¥ ―É―Ä–Ψ–≤–Ϋ–Β–Φ –Φ–Ψ―Ä―è. –ù–Α –≥–Ψ―Ä–Η–Ζ–Ψ–Ϋ―²–Α–Μ―¨–Ϋ–Ψ–Ι –Ψ―¹–Η –Ψ―²–Φ–Β―΅–Β–Ϋ–Α –≤―΄―¹–Ψ―²–Α –Ϋ–Α–¥ ―É―Ä–Ψ–≤–Ϋ–Β–Φ –Φ–Ψ―Ä―è –≤ –Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Α―Ö, –Ϋ–Α –≤–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ–Ψ–Ι βÄî –¥–Α–≤–Μ–Β–Ϋ–Η–Β –≤ –Φ–Η–Μ–Μ–Η–Φ–Β―²―Ä–Α―Ö ―Ä―²―É―²–Ϋ–Ψ–≥–Ψ ―¹―²–Ψ–Μ–±–Α. –û–Ω―Ä–Β–¥–Β–Μ–Η―²–Β –Ω–Ψ –≥―Ä–Α―³–Η–Κ―É, –Ϋ–Α –Κ–Α–Κ–Ψ–Ι –≤―΄―¹–Ψ―²–Β –Α―²–Φ–Ψ―¹―³–Β―Ä–Ϋ–Ψ–Β –¥–Α–≤–Μ–Β–Ϋ–Η–Β ―Ä–Α–≤–Ϋ–Ψ 280 –Φ–Η–Μ–Μ–Η–Φ–Β―²―Ä–Α–Φ ―Ä―²―É―²–Ϋ–Ψ–≥–Ψ ―¹―²–Ψ–Μ–±–Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Α―Ö.
–ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η
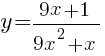
–û–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö k –Ω―Ä―è–Φ–Α―è y=kx –Η–Φ–Β–Β―² ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ ―Ä–Ψ–≤–Ϋ–Ψ –Ψ–¥–Ϋ―É –Ψ–±―â―É―é ―²–Ψ―΅–Κ―É.
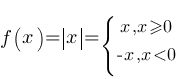
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: