
 В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
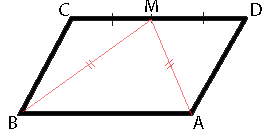
В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники BCM и MDA. CM=MD, т.к. точка M - середина CD, MA=MB (из условия задачи), CB=AD (по свойству параллелограмма). Соответственно, треугольники BCM и MDA равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что /BCM=/MDA.
BC||AD (по определению параллелограмма), рассмотрим сторону CD как секущую к этим параллельным сторонам. Тогда получается, что сумма углов BCM и MDA равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.
Теперь рассмотрим стороны AB и CD, они параллельны (тоже по определению параллелограмма). Рассмотрим сторону BC как секущую к этим параллельным сторонам.
/CBA и /MCB - внутренние односторонние. Следовательно их сумма равна 180°. А так как /MCB=90°, то /CBA тоже равен 90°.
Аналогично доказывается, что /DAB тоже равен 90°.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
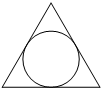 Сторона равностороннего треугольника равна 2√
Сторона равностороннего треугольника равна 2√
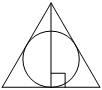 Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
 Катеты прямоугольного треугольника равны √
Катеты прямоугольного треугольника равны √
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
Комментарии: