ОГЭ, Математика.
Геометрия: Задача №E41C75

Задача №891 из 1087
Условие задачи:

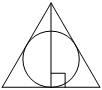
Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.

Решение задачи:

По свойству равностороннего треугольника:

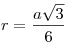
Тогда:
6r=a√3
a=6r/√3=6*5/√3= 30/√3=(3*10)/√3=((√3)²*10)/√3=10√3
По второму свойству равностороннего треугольника высота так же является и медианой.
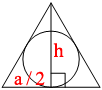Следовательно, она делит сторону, на которую опирается, пополам.
К тому же высота образует прямоугольный треугольник, следовательно, можно воспользоваться теоремой Пифагора:
a²=h²+(a/2)²
(10√3)²=h²+(10√3/2)²
100*3=h²+(5√3)²
300=h²+25*3
h²=300-75=225
h=√225=15
Ответ: 15

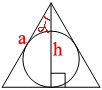Можно вместо теоремы Пифагора воспользоваться косинусом:
cosα=h/a (по определению).
По первому свойству равностороннего треугольника все углы равны 60°.
А по второму свойству, высота так же является и биссектрисой, т.е. делит угол пополам, следовательно α=60°/2=30°
По таблице косинусов:
√3/2=h/10√3
√3*10√3=2h
(√3)²*10=2h
3*10=2h
h=15
Ответ: 15

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №6A8458

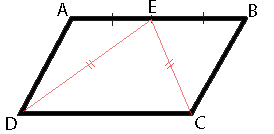В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.

Задача №B6B677

Найдите угол ABC. Ответ дайте в градусах.

Задача №3D1628

На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.