Постройте график функции y=x2-4|x|-2x и определите, при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
y=x2-4x-2x, при x≥0
y=x2-4(-x)-2x, при x<0
y=x2-6x, при x≥0
y=x2+2x, при x<0
Рассмотрим и построим график для каждой подфункции на определенном им диапазонах и объединим их.
График обеих подфункций - парабола, при чем, ветви параболы направлены вверх (так как коэффициент "а" больше нуля).
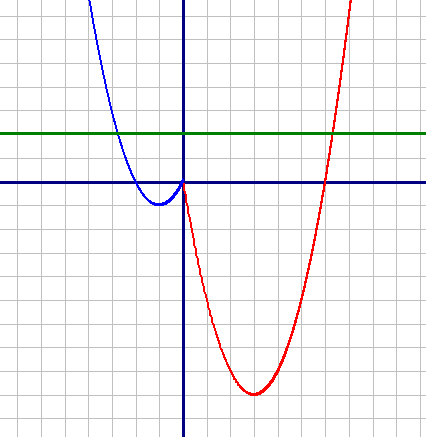Для первой подфункции (красная):
| X | 0 | 1 | 3 | 6 |
| Y | 0 | -5 | -9 | 0 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | -1 | 0 | 3 |
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 3-5*3-7/3-11.
1) -3
2) 3
3) 1/3
4) -1/3
Найдите значение выражения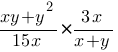 
при x=18; y=7,5.
Период колебания математического маятника (в секундах) приближённо можно вычислить по формуле T=2√
Какое из данных ниже чисел является значением выражения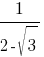 
?
1) -2-√3
2) √3-2
3) 2-√3
4) 2+√3
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 180 Вт, а сила тока равна 6 А.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-02-08 17:06:40) Администратор: Саша, так работает функция модуль, f(x)=|x|, f(x)=x, при x≥ и f(x)=-x, при x<0.
(2015-02-08 17:03:50) Саша: а почему y=x2-6x, при x≥0 y=x2+2x, при x<0