
При каких значениях р вершины парабол у=-х2+8рх+3 и у=х2-6рх+3р расположены по разные стороны от оси х?
Рассмотрим предложенные
квадратные уравнения:
В первом уравнении а=-1, т.е. меньше 0, значит ветви этой параболы направлены вниз;
во-втором уравнении а=1, т.е. больше 0, значит ветви направлены вверх.
Возможны два варианта:
1) Оба графика не пересекают ось х как на рисунке 1.
2) Оба графика пересекают ось х дважды, как на рисунке 2.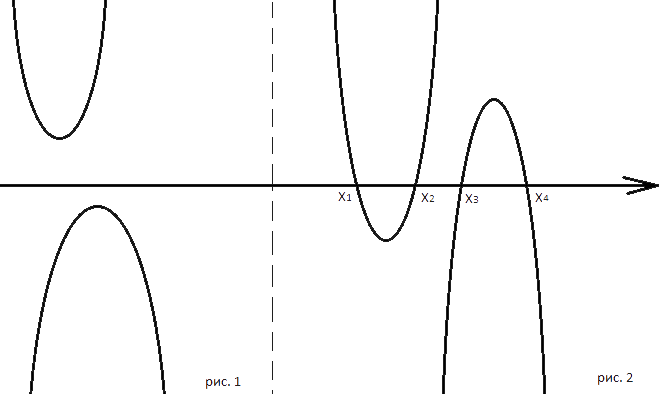
Рассмотрим каждый вариант:
1) Чтобы графики функций не пересекали ось х, уравнения функций не должны иметь
корней. Для
квадратного уравнения это означает, что
дискриминант меньше нуля.
у=-х2+8рх+3
D1=(8p)2-4*(-1)*3=64p2+12<0
64p2+12<0
64p2<-12
16p2<-3
p2<-3/16, это невозможно (квадрат числа всегда больше либо равен нулю).
Значит вариант первый отпадает (D2 для уравнения у=х2-6рх+3р можно даже вычислять).
2) Рассмотрим второй вариант, для второго варианта
дискриминант должен быть строго больше нуля:
у=-х2+8рх+3
D1=(8p)2-4*(-1)*3=64p2+12>0 => p2>-3/16, это неравенство выполняется для любого p
у=х2-6рх+3р
D2=(-6p)2-4*1*3p=36p2-12p>0, решим это неравенство.
36p2-12p>0
12(3p2-p)>0
3p2-p>0
p(3p-1)>0
Чтобы это неравенство выполнялось должно быть:
1) или p>0 и 3p-1>0
2) или p<0 и 3p-1<0
1) p>0 и p>1/3 => p>1/3
2) p<0 и p<1/3 => p<0
Ответ: p=(-∞;0)∪(1/3;+∞)
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 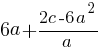 при a=12, с=15.
при a=12, с=15.
Найдите значение выражения (a+3)2-a(a-6) при a=-1/12.
Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s=nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l=80 см, n=1600? Ответ выразите в километрах.
Найдите значение выражения 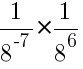
Найдите значение выражения 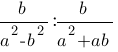 при a=1,1 и b=0,9.
при a=1,1 и b=0,9.
Комментарии: