Найдите p и постройте график функции y=x2+p, если известно, что прямая y=-2x имеет с графиком ровно одну общую точку.
Две функции имеют точку пересечения, это означает, что графики обеих функций имеют общую точку. Следовательно, надо составить систему и решить ее:
y=x2+p
y=-2x
-2x=x2+p
x2+2x+p=0
Найдем корни этого квадратного уравнения:
D=22-4*1*p=4-4p
В условии сказано, что точка пересечения только одна, следовательно корень уравнения должен быть только один. Это условие выполняется, когда дискриминант равен нулю:
D=4-4p=0
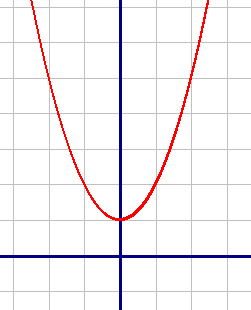
p=1
x=-2/(2*1)=-1
y=-2x=-2*(-1)=2
(-1;2) - точка пересечения графиков.
Получаем функцию:
y=x2+1
График функции:
Поделитесь решением
Присоединяйтесь к нам...
Для приготовления фарша взяли говядину и свинину в отношении 5:3. Какой процент в фарше составляет свинина?
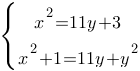
Решите уравнение -3x2+4x-7=-x2+5x-(-1+2x2).
Решите неравенство 2x2+x<0.
Решите неравенство (x-7)2<√
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 105 человек. Голоса между кандидатами распределились в отношении 2:5. Сколько голосов получил победитель?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: