Найдите p и постройте график функции y=x2+p, если известно, что прямая y=4x имеет с графиком ровно одну общую точку.
Две функции имеют точку пересечения, это означает, что графики обеих функций имеют общую точку. Следовательно, надо составить систему и решить ее:
y=x2+p
y=4x
4x=x2+p
x2-4x+p=0
Найдем корни этого
квадратного уравнения:
D=(-4)2-4*1*p=16-4p
В условии сказано, что точка пересечения только одна, следовательно корень уравнения должен быть только один. Это условие выполняется, когда дискриминант равен нулю:
D=16-4p=0
16=4p
p=4
x=-(-4)/(2*1)=2
y=4x=4*2=8
(2;8) - точка пересечения графиков.
Получаем функцию:
y=x2+4
График функции:
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) a>0, c<0 2) a<0, c<0 3) a>0, c>0 4) a<0, c>0 |
А)  |
Б)  |
В)  |
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
А)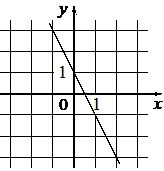 
Б) 
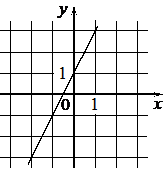В)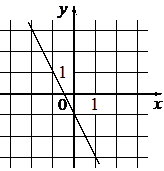 
ФОРМУЛЫ
1) y=-2x-1
2) y=-2x+1
3) y=2x+1
В таблице под каждой буквой укажите соответствующий номер.
При работе фонарика батарейка постепенно разряжается, и напряжение
в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, за сколько часов напряжение упадёт с 1,4 вольта до 0,8 вольта.
Постройте график функции
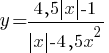
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1 В до 0,8 В.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-04-09 12:54:47) Администратор: Я добавил строчку в решение, чтобы стало понятно, просто решил уравнение 16-4p=0.
(2015-04-09 12:51:07) : как вы узнали, что р=4?
(2014-05-29 16:42:24) Администратор: Мария, не понял, где подписывать?
(2014-05-29 15:43:56) Мария: графики надо подписывать?