
Постройте график функции y=2|x-5|-x2+11x-30 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
 2(x-5)-x2+11x-30, при x-5≥0
2(x-5)-x2+11x-30, при x-5≥0
-2(x-5)-x2+11x-30, при x-5<0
 2x-10-x2+11x-30, при x≥5
2x-10-x2+11x-30, при x≥5
-2x+10-x2+11x-30, при x<5
 -x2+13x-40, при x≥5
-x2+13x-40, при x≥5
-x2+9x-20, при x<5
Теперь построим графики обеих подфункций в определенных для них диапазонах, для этого найдем корни этих подфункций через
дискриминант:
1) -x2+13x-40=0
D=132-4(-1)(-40)=169-160=9
x1=(-13+3)/(2(-1))=5
x2=(-13-3)/(2(-1))=8
2) -x2+9x-20=0
D=92-4(-1)*20=81-80=1
x1=(-9+1)/(2(-1))=4
x2=(-9-1)/(2(-1))=5
Так как коэффициент а=-1 (т.е. меньше нуля), значит ветви параболы направлены вниз.
Теперь можем построить график:
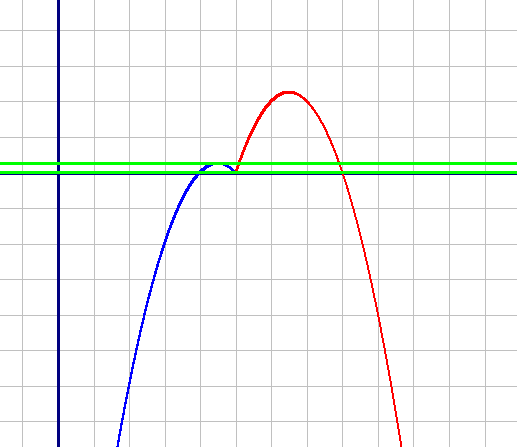 Первая подфункция - красная:
Первая подфункция - красная:
| X | 5 | 6 | 7 | 8 | 9 |
| Y | 0 | 2 | 2 | 0 | -4 |
| X | 5 | 4 | 3 | 2 |
| Y | 0 | 0 | -2 | -6 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
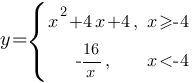
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Постройте график функции 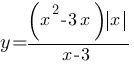 и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
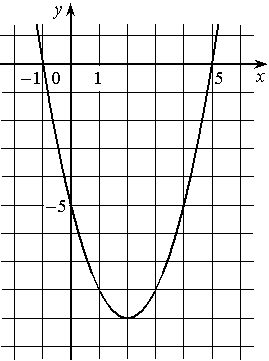 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) f(-1)=f(5)
2) Функция убывает на промежутке [2; +∞)
3) f(x)>0 при x<-1 и при x>5
Постройте график функции:
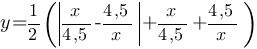 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Постройте график функции 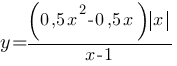 и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Комментарии:
(2015-03-31 21:13:20) Администратор: Лена, справедливое замечание. В решение добавлены таблицы координат.
(2015-03-31 17:55:41) Лена : Так как коэффициент а=-1 (т.е. меньше нуля), значит ветви параболы направлены вниз. p.s вот до сюда всё понятно,а дальше,по каким координатам, строим график?