
Постройте график функции
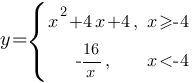
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Чтобы построить график функции состоящей из двух подфункций, необходимо построить график каждой подфункции на указанных для них диапазонах и объединить эти графики.
Первая подфункция - парабола. Так как коэффициент а больше нуля, то ветви параболы направлены вверх.
Вторая подфункция - гипербола.
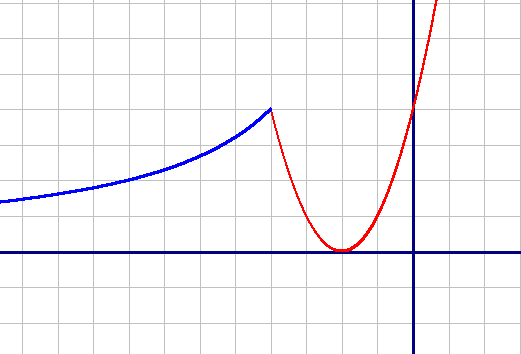 Построим по точкам график обоих подфункций в указанных диапазонах.
Построим по точкам график обоих подфункций в указанных диапазонах.
Для y1=x2+4x+4 (красный график)
| X | -4 | -2 | 0 | 1 |
| Y | 4 | 0 | 4 | 8 |
| X | -16 | -8 | -4 |
| Y | 1 | 2 | 4 |
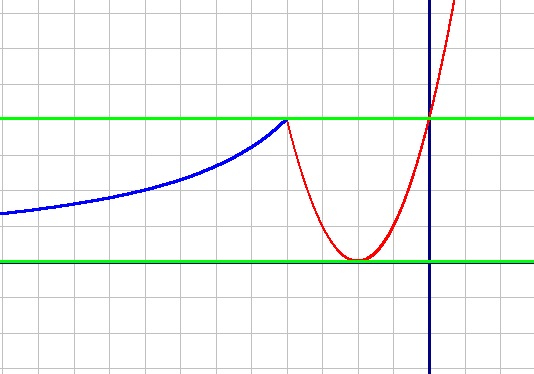 Зеленые прямые показывают, где прямая y=m имеет с графиком одну или две общие точки. Т.е. m=0 и m≥4.
Ответ: m⊂0∪[4;+∞)
Зеленые прямые показывают, где прямая y=m имеет с графиком одну или две общие точки. Т.е. m=0 и m≥4.
Ответ: m⊂0∪[4;+∞) Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=x2-5|x|-x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
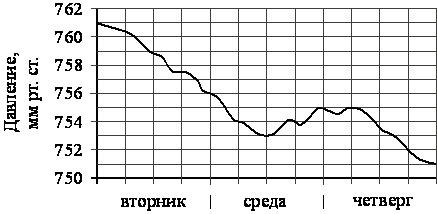 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник (мм рт. ст.).
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник (мм рт. ст.).
Постройте график функции
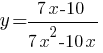 .
.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
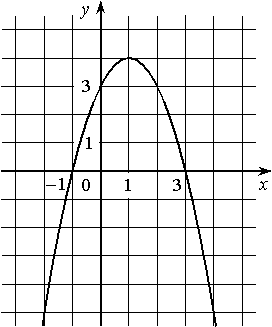 На рисунке изображён график квадратичной функции y=ƒ(x).
На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) ƒ(x)<0 при x<1
2) Наибольшее значение функции равно 3
3) ƒ(0)>ƒ(4)
Постройте график функции y=|x|x+|x|-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Комментарии:
(2016-02-17 12:53:30) Администратор: Владимир, в условии сказано "одну или две", при m>4 прямая тоже будет пересекаться с графиком в одной точке, это видно из самого графика. Он уходит вверх, в бесконечность, поэтому любая горизонтальная прямая будет с ним пересекаться.
(2016-02-16 20:47:46) Владимир: Поясните пожалуйста почему ответ не m=0 и m=4