
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ15 –Η–Ζ 287 |
–ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η 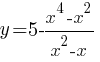 –Η –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö m –Ω―Ä―è–Φ–Α―è y=m –Η–Φ–Β–Β―² ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ ―Ä–Ψ–≤–Ϋ–Ψ –¥–≤–Β –Ψ–±―â–Η–Β ―²–Ψ―΅–Κ–Η.
–Η –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö m –Ω―Ä―è–Φ–Α―è y=m –Η–Φ–Β–Β―² ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ ―Ä–Ψ–≤–Ϋ–Ψ –¥–≤–Β –Ψ–±―â–Η–Β ―²–Ψ―΅–Κ–Η.
–û–±–Μ–Α―¹―²―¨ –î–Ψ–Ω―É―¹―²–Η–Φ―΄―Ö –½–Ϋ–Α―΅–Β–Ϋ–Η–Ι (–û–î–½):
x2-x≠0, ―².–Κ. –Ϋ–Α –Ϋ–Ψ–Μ―¨ –¥–Β–Μ–Η―²―¨ –Ϋ–Β–Μ―¨–Ζ―è.
x(x-1)≠0
x1≠0
x2≠1
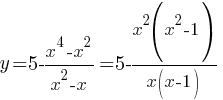

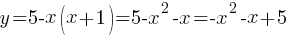
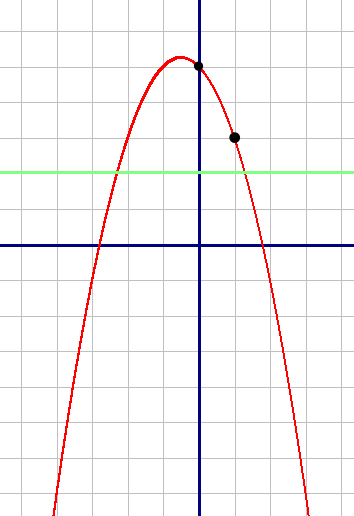 –™―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η - –Ω–Α―Ä–Α–±–Ψ–Μ–Α, ―²–Α–Κ –Κ–Α–Κ –Κ–Ψ―ç―³―³–Η―Ü–Η–Β―² "–Α" ―Ä–Α–≤–Β–Ϋ -1, ―².–Β. –Φ–Β–Ϋ―¨―à–Β –Ϋ―É–Μ―è, ―²–Ψ –≤–Β―²–≤–Η –Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ―΄ –≤–Ϋ–Η–Ζ.
–™―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η - –Ω–Α―Ä–Α–±–Ψ–Μ–Α, ―²–Α–Κ –Κ–Α–Κ –Κ–Ψ―ç―³―³–Η―Ü–Η–Β―² "–Α" ―Ä–Α–≤–Β–Ϋ -1, ―².–Β. –Φ–Β–Ϋ―¨―à–Β –Ϋ―É–Μ―è, ―²–Ψ –≤–Β―²–≤–Η –Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ―΄ –≤–Ϋ–Η–Ζ.| X | -2 | -1 | 0 | 1 | 2 |
| Y | 3 | 5 | 5 | 3 | -1 |
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
–ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η y=x2-6|x|+2x –Η –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö c –Ω―Ä―è–Φ–Α―è y=c –Η–Φ–Β–Β―² ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ ―Ä–Ψ–≤–Ϋ–Ψ ―²―Ä–Η –Ψ–±―â–Η–Β ―²–Ψ―΅–Κ–Η.
–ù–Α ―Ä–Η―¹―É–Ϋ–Κ–Β –Η–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ―΄ –≥―Ä–Α―³–Η–Κ–Η ―³―É–Ϋ–Κ―Ü–Η–Ι –≤–Η–¥–Α y=kx+b. –Θ―¹―²–Α–Ϋ–Ψ–≤–Η―²–Β ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Φ–Β–Ε–¥―É –≥―Ä–Α―³–Η–Κ–Α–Φ–Η ―³―É–Ϋ–Κ―Ü–Η–Ι –Η –Ζ–Ϋ–Α–Κ–Α–Φ–Η –Κ–Ψ―ç―³―³–Η―Ü–Η–Β–Ϋ―²–Ψ–≤ k –Η b.
| –ö–û–≠–Λ–Λ–‰–Π–‰–ï–ù–Δ–Ϊ | –™–†–ê–Λ–‰–ö–‰ | ||
|
1) k<0, b<0 2) k<0, b>0 3) k>0, b>0 4) k>0, b<0 |
–ê)  |
–ë)  |
–£)  |
–Θ―¹―²–Α–Ϋ–Ψ–≤–Η―²–Β ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Φ–Β–Ε–¥―É ―³―É–Ϋ–Κ―Ü–Η―è–Φ–Η –Η –Η―Ö –≥―Ä–Α―³–Η–Κ–Α–Φ–Η.
–Λ–Θ–ù–ö–Π–‰–‰
–ê) y=-2x+4
–ë) y=2x-4
–£) y=2x+4
–™–†–ê–Λ–‰–ö–‰
1) 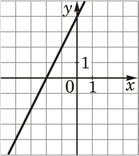 2)
2) 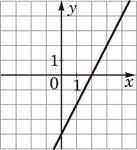 3)
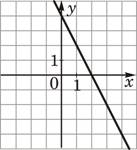
3) 
–£ ―²–Α–±–Μ–Η―Ü–Β –Ω–Ψ–¥ –Κ–Α–Ε–¥–Ψ–Ι –±―É–Κ–≤–Ψ–Ι ―É–Κ–Α–Ε–Η―²–Β ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤―É―é―â–Η–Ι –Ϋ–Ψ–Φ–Β―Ä.
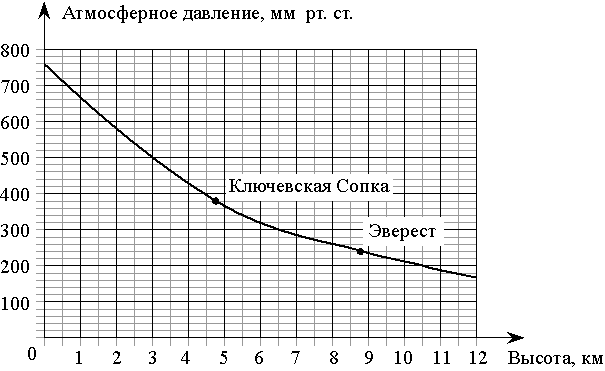 –ù–Α –≥―Ä–Α―³–Η–Κ–Β –Η–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Α –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―²―¨ –Α―²–Φ–Ψ―¹―³–Β―Ä–Ϋ–Ψ–≥–Ψ –¥–Α–≤–Μ–Β–Ϋ–Η―è (–≤ –Φ–Η–Μ–Μ–Η–Φ–Β―²―Ä–Α―Ö ―Ä―²―É―²–Ϋ–Ψ–≥–Ψ ―¹―²–Ψ–Μ–±–Α) –Ψ―² –≤―΄―¹–Ψ―²―΄ –Φ–Β―¹―²–Ϋ–Ψ―¹―²–Η –Ϋ–Α–¥ ―É―Ä–Ψ–≤–Ϋ–Β–Φ –Φ–Ψ―Ä―è (–≤ –Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Α―Ö). –ù–Α ―¹–Κ–Ψ–Μ―¨–Κ–Ψ –Φ–Η–Μ–Μ–Η–Φ–Β―²―Ä–Ψ–≤ ―Ä―²―É―²–Ϋ–Ψ–≥–Ψ ―¹―²–Ψ–Μ–±–Α –Α―²–Φ–Ψ―¹―³–Β―Ä–Ϋ–Ψ–Β –¥–Α–≤–Μ–Β–Ϋ–Η–Β –Ϋ–Α –≤―΄―¹–Ψ―²–Β –≠–≤–Β―Ä–Β―¹―²–Α –Ϋ–Η–Ε–Β –Α―²–Φ–Ψ―¹―³–Β―Ä–Ϋ–Ψ–≥–Ψ –¥–Α–≤–Μ–Β–Ϋ–Η―è –Ϋ–Α –≤―΄―¹–Ψ―²–Β –ö–Μ―é―΅–Β–≤―¹–Κ–Ψ–Ι –Γ–Ψ–Ω–Κ–Η?
–ù–Α –≥―Ä–Α―³–Η–Κ–Β –Η–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Α –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―²―¨ –Α―²–Φ–Ψ―¹―³–Β―Ä–Ϋ–Ψ–≥–Ψ –¥–Α–≤–Μ–Β–Ϋ–Η―è (–≤ –Φ–Η–Μ–Μ–Η–Φ–Β―²―Ä–Α―Ö ―Ä―²―É―²–Ϋ–Ψ–≥–Ψ ―¹―²–Ψ–Μ–±–Α) –Ψ―² –≤―΄―¹–Ψ―²―΄ –Φ–Β―¹―²–Ϋ–Ψ―¹―²–Η –Ϋ–Α–¥ ―É―Ä–Ψ–≤–Ϋ–Β–Φ –Φ–Ψ―Ä―è (–≤ –Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Α―Ö). –ù–Α ―¹–Κ–Ψ–Μ―¨–Κ–Ψ –Φ–Η–Μ–Μ–Η–Φ–Β―²―Ä–Ψ–≤ ―Ä―²―É―²–Ϋ–Ψ–≥–Ψ ―¹―²–Ψ–Μ–±–Α –Α―²–Φ–Ψ―¹―³–Β―Ä–Ϋ–Ψ–Β –¥–Α–≤–Μ–Β–Ϋ–Η–Β –Ϋ–Α –≤―΄―¹–Ψ―²–Β –≠–≤–Β―Ä–Β―¹―²–Α –Ϋ–Η–Ε–Β –Α―²–Φ–Ψ―¹―³–Β―Ä–Ϋ–Ψ–≥–Ψ –¥–Α–≤–Μ–Β–Ϋ–Η―è –Ϋ–Α –≤―΄―¹–Ψ―²–Β –ö–Μ―é―΅–Β–≤―¹–Κ–Ψ–Ι –Γ–Ψ–Ω–Κ–Η?
–ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η
 -x2, –Β―¹–Μ–Η |x|≤1
-x2, –Β―¹–Μ–Η |x|≤1
1/x, –Β―¹–Μ–Η |x|>1
–Η –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö c –Ω―Ä―è–Φ–Α―è y=c –±―É–¥–Β―² –Η–Φ–Β―²―¨ ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ –Β–¥–Η–Ϋ―¹―²–≤–Β–Ϋ–Ϋ―É―é –Ψ–±―â―É―é ―²–Ψ―΅–Κ―É.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2017-03-17 02:59:14) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –¦―é–¥–Φ–Η–Μ–Α, ―¹–Ω–Α―¹–Η–±–Ψ –±–Ψ–Μ―¨―à–Ψ–Β, ―΅―²–Ψ –Ζ–Α–Φ–Β―²–Η–Μ–Η –Ϋ–Β―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β. –· –Η―¹–Ω―Ä–Α–≤–Η–Μ ―Ä–Β―à–Β–Ϋ–Η–Β.
(2017-03-16 19:24:07) –¦―é–¥–Φ–Η–Μ–Α: –£―΄ –≤―΄–Ϋ–Ψ―¹–Η―²–Β –Ζ–Α ―¹–Κ–Ψ–±–Κ―É ―΅–Η―¹–Μ–Η―²–Β–Μ―è –Ξ^3, –Α ―΅–Η―¹–Μ–Η―²–Β–Μ―¨ X^4-X^2. –ù–Α–≤–Β―Ä–Ϋ–Ψ–Β –≤ ―É―¹–Μ–Ψ–≤–Η–Η –Ψ―à–Η–±–Κ–Α.