
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ6 –Є–Ј 1087 |
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ KLMN —В–Њ—З–Ї–∞ A вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л LM. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ KA=NA. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –і–∞–љ–љ—Л–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ вАФ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
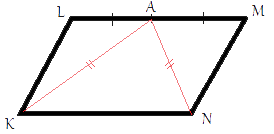 –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є KLA –Є NMA. LA=MA, —В.–Ї. —В–Њ—З–Ї–∞ –Р - —Б–µ—А–µ–і–Є–љ–∞ LM, AK=AN –Є–Ј —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞—З–Є, LK=MN (–њ–Њ —Б–≤–Њ–є—Б—В–≤—Г –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞). –°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є KLA –Є NMA —А–∞–≤–љ—Л (–њ–Њ —В—А–µ—В—М–µ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г —А–∞–≤–µ–љ—Б—В–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤).
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є KLA –Є NMA. LA=MA, —В.–Ї. —В–Њ—З–Ї–∞ –Р - —Б–µ—А–µ–і–Є–љ–∞ LM, AK=AN –Є–Ј —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞—З–Є, LK=MN (–њ–Њ —Б–≤–Њ–є—Б—В–≤—Г –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞). –°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є KLA –Є NMA —А–∞–≤–љ—Л (–њ–Њ —В—А–µ—В—М–µ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г —А–∞–≤–µ–љ—Б—В–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤).
–Ш–Ј —А–∞–≤–µ–љ—Б—В–≤–∞ —Н—В–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —Б–ї–µ–і—Г–µ—В, —З—В–Њ ∠KLA=∠NMA.
LK||MN (–њ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞), —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б—В–Њ—А–Њ–љ—Г LM –Ї–∞–Ї —Б–µ–Ї—Г—Й—Г—О –Ї —Н—В–Є–Љ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–Љ —Б—В–Њ—А–Њ–љ–∞–Љ. –Ґ–Њ–≥–і–∞ –њ–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ —Б—Г–Љ–Љ–∞ —Г–≥–ї–Њ–≤ KLA –Є NMA —А–∞–≤–љ–∞ 180¬∞, —В.–Ї. —Н—В–Є —Г–≥–ї—Л —П–≤–ї—П—О—В—Б—П –≤–љ—Г—В—А–µ–љ–љ–Є–Љ–Є –Њ–і–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–Љ–Є. –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ –Ї–∞–ґ–і—Л–є –Є–Ј —Н—В–Є—Е —Г–≥–ї–Њ–≤ —А–∞–≤–µ–љ 90¬∞.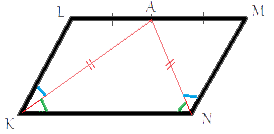 –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї KAN, KA=NA (–њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є), —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, —Н—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є. –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ ∠AKN=∠ANK (
–Є–Ј —Б–≤–Њ–є—Б—В–≤–∞ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞). –Ш–Ј —А–∞–љ–µ–µ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–≥–Њ —А–∞–≤–µ–љ—Б—В–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤, —Б–ї–µ–і—Г–µ—В, —З—В–Њ ∠LKA=∠MNA. –Я–Њ–ї—Г—З–∞–µ–Љ, —З—В–Њ —Г–≥–ї—Л LKN –Є MNK —А–∞–≤–љ—Л.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї KAN, KA=NA (–њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є), —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, —Н—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є. –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ ∠AKN=∠ANK (
–Є–Ј —Б–≤–Њ–є—Б—В–≤–∞ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞). –Ш–Ј —А–∞–љ–µ–µ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–≥–Њ —А–∞–≤–µ–љ—Б—В–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤, —Б–ї–µ–і—Г–µ—В, —З—В–Њ ∠LKA=∠MNA. –Я–Њ–ї—Г—З–∞–µ–Љ, —З—В–Њ —Г–≥–ї—Л LKN –Є MNK —А–∞–≤–љ—Л.
–Т —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М –Њ–љ–Є —В–∞–Ї –ґ–µ —П–≤–ї—П—О—В—Б—П –≤–љ—Г—В—А–µ–љ–љ–Є–Љ–Є –Њ–і–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–Љ–Є –Є –Є—Е —Б—Г–Љ–Љ–∞ —А–∞–≤–љ–∞ 180¬∞. –Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ –Є —Н—В–Є —Г–≥–ї—Л —А–∞–≤–љ—Л 90¬∞ –Ї–∞–ґ–і—Л–є.
–Я–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ, —Г –Ї–Њ—В–Њ—А–Њ–≥–Њ –≤—Б–µ —Г–≥–ї—Л –њ—А—П–Љ—Л–µ (—В.–µ. 90¬∞) –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ (–њ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О).
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т —В—А–∞–њ–µ—Ж–Є—О, —Б—Г–Љ–Љ–∞ –і–ї–Є–љ –±–Њ–Ї–Њ–≤—Л—Е —Б—В–Њ—А–Њ–љ –Ї–Њ—В–Њ—А–Њ–є —А–∞–≤–љ–∞ 18, –≤–њ–Є—Б–∞–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є —В—А–∞–њ–µ—Ж–Є–Є.
–Т —В—А–∞–њ–µ—Ж–Є—О, —Б—Г–Љ–Љ–∞ –і–ї–Є–љ –±–Њ–Ї–Њ–≤—Л—Е —Б—В–Њ—А–Њ–љ –Ї–Њ—В–Њ—А–Њ–є —А–∞–≤–љ–∞ 18, –≤–њ–Є—Б–∞–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є —В—А–∞–њ–µ—Ж–Є–Є.
 –Ю–і–Є–љ –Є–Ј —Г–≥–ї–Њ–≤ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ —А–∞–≤–µ–љ 111¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї —Н—В–Њ–≥–Њ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞. –Ю—В–≤–µ—В –і–∞–є—В–µ
–≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ю–і–Є–љ –Є–Ј —Г–≥–ї–Њ–≤ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ —А–∞–≤–µ–љ 111¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї —Н—В–Њ–≥–Њ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞. –Ю—В–≤–µ—В –і–∞–є—В–µ
–≤ –≥—А–∞–і—Г—Б–∞—Е.
 –†–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –Ї–≤–∞–і—А–∞—В –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 22√2. –Э–∞–є–і–Є—В–µ –і–Є–∞–≥–Њ–љ–∞–ї—М —Н—В–Њ–≥–Њ –Ї–≤–∞–і—А–∞—В–∞.
–†–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –Ї–≤–∞–і—А–∞—В –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 22√2. –Э–∞–є–і–Є—В–µ –і–Є–∞–≥–Њ–љ–∞–ї—М —Н—В–Њ–≥–Њ –Ї–≤–∞–і—А–∞—В–∞.
 –Ф–≤–µ –Ї–∞—Б–∞—О—Й–Є–µ—Б—П –≤–љ–µ—И–љ–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –≤ —В–Њ—З–Ї–µ K –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —А–∞–і–Є—Г—Б—Л –Ї–Њ—В–Њ—А—Л—Е —А–∞–≤–љ—Л 39 –Є 42, –≤–њ–Є—Б–∞–љ—Л –≤ —Г–≥–Њ–ї —Б –≤–µ—А—И–Є–љ–Њ–є A. –Ю–±—Й–∞—П –Ї–∞—Б–∞—В–µ–ї—М–љ–∞—П –Ї —Н—В–Є–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—П–Љ, –њ—А–Њ—Е–Њ–і—П—Й–∞—П —З–µ—А–µ–Ј —В–Њ—З–Ї—Г K, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л —Г–≥–ї–∞ –≤ —В–Њ—З–Ї–∞—Е B –Є C. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Ф–≤–µ –Ї–∞—Б–∞—О—Й–Є–µ—Б—П –≤–љ–µ—И–љ–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –≤ —В–Њ—З–Ї–µ K –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —А–∞–і–Є—Г—Б—Л –Ї–Њ—В–Њ—А—Л—Е —А–∞–≤–љ—Л 39 –Є 42, –≤–њ–Є—Б–∞–љ—Л –≤ —Г–≥–Њ–ї —Б –≤–µ—А—И–Є–љ–Њ–є A. –Ю–±—Й–∞—П –Ї–∞—Б–∞—В–µ–ї—М–љ–∞—П –Ї —Н—В–Є–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—П–Љ, –њ—А–Њ—Е–Њ–і—П—Й–∞—П —З–µ—А–µ–Ј —В–Њ—З–Ї—Г K, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л —Г–≥–ї–∞ –≤ —В–Њ—З–Ї–∞—Е B –Є C. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
 –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —А–Њ–Љ–±–∞, –µ—Б–ї–Є –µ–≥–Њ –і–Є–∞–≥–Њ–љ–∞–ї–Є —А–∞–≤–љ—Л 39 –Є 2.
–Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —А–Њ–Љ–±–∞, –µ—Б–ї–Є –µ–≥–Њ –і–Є–∞–≥–Њ–љ–∞–ї–Є —А–∞–≤–љ—Л 39 –Є 2.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2019-03-31 11:20:50) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Х–ї–µ–љ–∞, –∞ –Ї–∞–Ї –Т—Л –≤—Л—З–Є—Б–ї–Є–ї–Є, —З—В–Њ —Г–≥–Њ–ї KLM –њ—А—П–Љ–Њ–є?
(2019-03-28 21:01:57) –Х–ї–µ–љ–∞: —В–∞–Ї –Ї–∞–Ї LM II KN (–њ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞), LK - —Б–µ–Ї—Г—Й–∞—П, —В–Њ —Б—Г–Љ–Љ–∞ –Њ–і–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є—Е —Г–≥–ї–Њ–≤ –ЪLM –Є LKM —А–∞–≤–љ–∞ 180 –≥—А–∞–і—Г—Б–∞–Љ. –Ч–љ–∞—З–Є—В, —Г–≥–Њ–ї LKM = 180 - 90 = 90.–£–≥–Њ–ї –ЪN–Ь –љ–∞—Е–Њ–і–Є–Љ –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ.
(2017-03-29 11:10:09) –Р—А–Є–љ–∞: –°–њ–∞—Б–Є–±–Њ –±–Њ–ї—М—И–Њ–µ!!–Т–∞—Б —Б–∞–є—В –Љ–љ–µ –Њ—З–µ–љ—М –њ–Њ–Љ–Њ–≥–∞–µ—В.
(2017-03-21 20:47:45) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Х–≤–≥–µ–љ–Є–є, –і–∞, –Љ–Њ–ґ–љ–Њ –Є —В–∞–Ї.
(2017-03-21 08:27:03) –Х–≤–≥–µ–љ–Є–є: –Р –љ–µ–ї—М–Ј—П –њ–Њ—Б–ї–µ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–∞ —А–∞–≤–µ–љ—Б—В–≤–∞ —Г–≥–ї–Њ–≤ KLA=NMA=90 —Б–Ї–∞–Ј–∞—В—М,—З—В–Њ —Г–≥–Њ–ї KLA=KNM, –∞ —Г–≥–Њ–ї NMA=LKN(–њ–Њ —Б–≤–Њ–є—Б—В–≤—Г –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞) —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Г–≥–Њ–ї KNM=LKN=90
(2015-03-21 15:41:45) –Р–љ–љ–∞: –њ—А–µ–Ї—А–∞—Б–љ–Њ!!!!!!
(2014-11-28 02:25:10) –С–∞–ї–Њ–±–Є–љ–∞ –Х–≥–Њ—А: –Я—А–Њ—Б—В–Њ –Ј–∞–Љ–µ—З–∞—В–µ–ї—М–љ–Њ! –°—Г–њ–µ—А!!
(2014-05-30 15:48:44) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ь–∞—А–Є—П, –љ—Г –љ–∞–≤–µ—А–љ–Њ, –љ–µ —Б–Њ–≤—Б–µ–Љ –≤—Б–µ. –Ч–і–µ—Б—М –Љ–љ–Њ–≥–Њ –њ–Њ–і—А–Њ–±–љ—Л—Е –Њ–±—К—П—Б–љ–µ–љ–Є–є, –Ї–Њ—В–Њ—А—Л–µ –љ–µ–Њ–±—П–Ј–∞—В–µ–ї—М–љ—Л, –∞ –і–∞–љ—Л —В–Њ–ї—М–Ї–Њ –і–ї—П –њ–Њ–љ–Є–Љ–∞–љ–Є—П —Е–Њ–і–∞ —А–µ—И–µ–љ–Є—П. –Э–Њ –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ —Б—Б—Л–ї–∞—В—М—Б—П –љ–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П, —В–µ–Њ—А–µ–Љ—Л, –∞–Ї—Б–Є–Њ–Љ—Л –Є —В.–і.
(2014-05-30 15:26:18) –Ь–∞—А–Є—П: –Р –µ—Б–ї–Є –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–µ —Н—В–∞ –Ј–∞–і–∞—З–∞ –±—Г–і–µ—В —Н—В–Њ –≤—Б–µ –њ–Є—Б–∞—В—М –љ–∞–і–Њ?
(2014-05-09 13:44:45) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т —Б–∞–Љ–Њ–Љ –љ–∞—З–∞–ї–µ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–∞, –≤—Л–≤–Њ–і–Є—В—Б—П —А–∞–≤–µ–љ—Б—В–≤–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ KLA –Є NMA, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —А–∞–≤–љ—Л –Є—Е —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ —Г–≥–ї—Л.
(2014-05-09 11:33:05) —О–ї–Є—П:: —П –љ–µ –њ–Њ–љ—П–ї–∞ /KLA=/NMA.