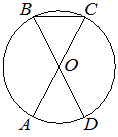
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.
∠AOB -
смежный углу AOD. Следовательно:
∠AOB=180°-∠AOD=180°-50°=130°
∠AOB является
центральным, и следовательно равен градусной мере дуги, на которую опирается.
∠ACB -
вписанный угол, и следовательно равен половине градусной меры дуги, на которую он опирается.
∠ACB=130°/2=65°
Ответ: 65
Поделитесь решением
Присоединяйтесь к нам...
Радиус окружности с центром в точке O равен 29, длина хорды AB равна 40 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
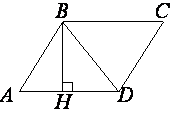Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Из вершины прямого угла C треугольника
ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: