
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
Рассмотрим каждое утверждение.
1) Есть
теорема об окружности, описанной около треугольника. Т.е. утверждение верно.
2) По
свойству квадрата это утверждение верно.
3) Площадь
трапеции равна произведению средней линии на высоту. Это утверждение тоже верно.
Поделитесь решением
Присоединяйтесь к нам...
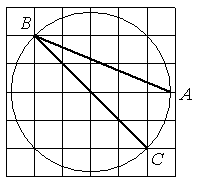 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
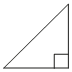 В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
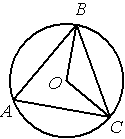 Точка О – центр окружности, /BAC=60° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=60° (см. рисунок). Найдите величину угла BOC (в градусах).
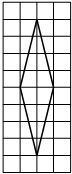 На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
Комментарии:
(2017-04-16 14:12:05) Троишник: СПАСИБ!!!!!!
(2016-02-03 13:23:08) : :-)
(2015-12-17 10:05:01) : КЛАСС
(2015-12-06 12:50:43) Пятерка: :*
(2015-12-06 12:50:24) Ангелочек: СУПЕР!!!:)))