Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
Площадь
трапеции вычисляется по формуле 
, где a и b - основания трапеции, а h - высота трапеции. Обозначим углы трапеции A, B, C и D. И проведем высоту из угла B к основанию AD, как паказано на рисунке.
Получившийся треугольник ABP -
прямоугольный c катетами BP и AP. Заметим, что BP - это катет притиволежащий углу в 30°, следовательно он равен половине гипотенузы (
по свойству прямоугольного треугольника), h=3/2=1,5. Используя формулу площади трапеции получаем S=(2+6)*1,5/2. Вычисляем S=6.
Ответ: S=6.
Поделитесь решением
Присоединяйтесь к нам...
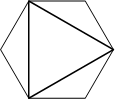Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 163°. Найдите угол C. Ответ дайте в градусах.
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-02-06 21:50:52) Дарья: Спасибо огромное автору и сайту за проделанную работу.Это очень помогает и выручает в той ситуации,когда не можешь решить то или иное задание.Спасибо!