Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
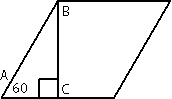Рассмотрим треугольник АВС, этот треугольник
прямоугольный (по условию задачи). /A=60°, следовательно по
теореме о сумме углов треугольника /АВС = 180°-90°-60°=30°. По
свойству прямоугольного треугольника АС=АВ/2=30/2=15. Следовательно вторая половина стороны ромба = 30-15=15. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: длины обоих отрезков равны 15.
Поделитесь решением
Присоединяйтесь к нам...
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
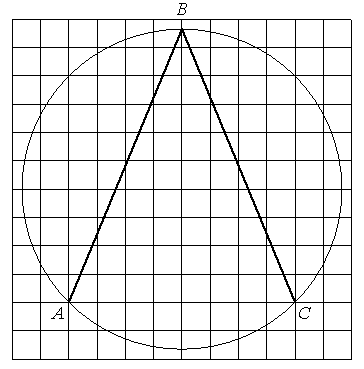Найдите угол ABC. Ответ дайте в градусах.
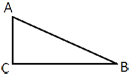Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 39.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-03-05 20:16:42) Администратор: Сэм, почему такой ответ показано в решении, а вот почему у Вас другой ответ - сказать не смогу пока не увижу Ваше решение.
(2016-03-04 17:13:22) сэм: почему такой ответ у меня получилось по другому