
 Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
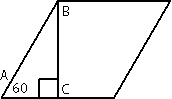 Рассмотрим треугольник АВС, этот треугольник
прямоугольный (по условию задачи). /A=60°, следовательно по
теореме о сумме углов треугольника /АВС = 180°-90°-60°=30°. По
свойству прямоугольного треугольника АС=АВ/2=30/2=15. Следовательно вторая половина стороны ромба = 30-15=15. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Рассмотрим треугольник АВС, этот треугольник
прямоугольный (по условию задачи). /A=60°, следовательно по
теореме о сумме углов треугольника /АВС = 180°-90°-60°=30°. По
свойству прямоугольного треугольника АС=АВ/2=30/2=15. Следовательно вторая половина стороны ромба = 30-15=15. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: длины обоих отрезков равны 15.
Поделитесь решением
Присоединяйтесь к нам...
 Площадь прямоугольного треугольника равна 968√
Площадь прямоугольного треугольника равна 968√
 В трапеции ABCD известно, что AD=4, BC=2, а её площадь равна 69. Найдите площадь треугольника ABC.
В трапеции ABCD известно, что AD=4, BC=2, а её площадь равна 69. Найдите площадь треугольника ABC.
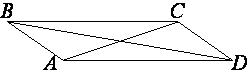 В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
 Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
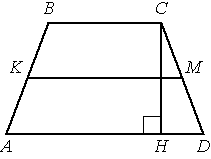 В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
Комментарии:
(2016-03-05 20:16:42) Администратор: Сэм, почему такой ответ показано в решении, а вот почему у Вас другой ответ - сказать не смогу пока не увижу Ваше решение.
(2016-03-04 17:13:22) сэм: почему такой ответ у меня получилось по другому