
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны
AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны
AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
BM -
медиана треугольника АВС,
следовательно, она делит этот треугольник на два равных по площади треугольника (
свойство медианы).
SABM=SCMB=SABC/2
Рассмотрим треугольник ABM.
SABK+SAKM=SABM=SABC/2
AP -
биссектриса, по
теореме о биссектрисе можно записать AM/AB=KM/BK.
По условию задачи AC втрое больше AB, следовательно, AM в 1,5 раза больше АВ (т.к. является половиной АС)
KM/BK=1,5. Т.к. площадь треугольника вычисляется по формуле S=1/2*h*a, где а-основание и h-высота,
то можем записать:
SAKM=1/2*h*KM=1/2*h*(1,5*BK),
SAKM=1/2*h*(3/2*BK)=3/2*(1/2*h*BK)=3/2*SABK (т.к. высота h для этих треугольников общая)
SABK=2/3*SAKM
SABK+SAKM=SABM=SABC/2
2/3*SAKM+SAKM=SABC/2
5/3*SAKM=SABC/2
SAKM=0,3*SABC
По тому же
свойству биссектрисы для треугольника ABC получаем, что AC/AB=CP/PB
AC/AB=3 (по условию задачи), следовательно, CP=3*PB
SAPC=1/2*h*PC=1/2*h*(3*PB)=3*(1/2*h*PB)=3*SABP,
SABP+SAPC=SABC
SABP+3*SABP=SABC
SABP=SABC/4
SKPCM=SABC-SABP-SAKM=SABC-SABC/4-0,3*SABC=0,45*SABC
Ответ: Отношение SKPCM к SABC равно 0,45.
Поделитесь решением
Присоединяйтесь к нам...
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
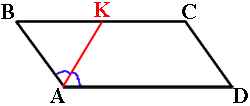 Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
 Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
Какой угол (в градусах) описывает часовая стрелка за 2 часа 2 минуты?
Комментарии:
(2015-06-06 08:46:57) лида: Спасибо:)