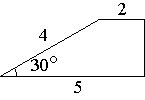
Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
Площадь
трапеции вычисляется по формуле 
, где a и b - основания трапеции,
а h - высота трапеции. Обозначим углы трапеции A, B, C и D. И проведем высоту из угла B к основанию AD, как паказано на рисунке.
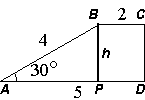Получившийся треугольник ABP -
прямоугольный c катетами BP и AP. Заметим, что BP - это катет притиволежащий углу в 30°, следовательно он равен половине
гипотенузы (
по свойству прямоугольного треугольника), h=4/2=2. Используя формулу площади трапеции получаем S=(2+5)*2/2.
Вычисляем S=7.
Ответ: S=7.
Поделитесь решением
Присоединяйтесь к нам...
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Человек ростом 1,5 м стоит на расстоянии 7 м от столба, на котором висит фонарь на высоте 3,6 м. Найдите длину тени человека в метрах.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-25 18:11:21) Lina: Огромное спасибо
(2015-05-21 18:06:36) Динар: Спасибо
(2015-05-16 09:40:34) : SPS
(2015-03-21 16:07:42) Анна: замечательно!!!!