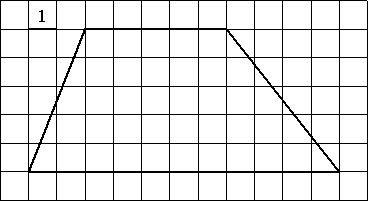
Найдите площадь трапеции, изображённой на рисунке.
Площадь трапеции равна произведению полусуммы оснований на высоту. Вычисляем:
Sтрапеции=5*(5+11)/2=40.
Ответ: Sтрапеции=40.
Поделитесь решением
Присоединяйтесь к нам...
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
В треугольнике ABC угол C прямой, BC=8, cosB=0,8. Найдите AB.
В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 72°. Найдите величину угла OMK. Ответ дайте в градусах.
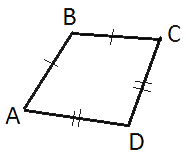В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: