
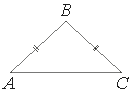
 В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB.
В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB.
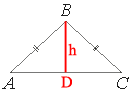 Проведем высоту к основанию треугольника.
Проведем высоту к основанию треугольника.
Площадь треугольника:
S=(1/2)AC*h
300=(1/2)40*h
300=(40/2)*h
300=20h
h=15=BD
Так как h - высота, то треугольник ABD -
прямоугольный.
Тогда мы можем воспользоваться
теоремой Пифагора:
AB2=BD2+AD2
Но нам неизвестна AD.
По третьему свойству
равнобедренного треугольника,
высота является так же и
медианой, следовательно:
AD=AC/2=40/2=20
Подставляем значения в теорему Пифагора:
AB2=152+202
AB2=225+400=625
AB=√625=25
Ответ: 25
Поделитесь решением
Присоединяйтесь к нам...
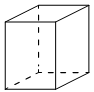 Два ребра прямоугольного параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
Два ребра прямоугольного параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
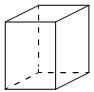 Два ребра прямоугольного параллелепипеда равны 8 и 2, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
Два ребра прямоугольного параллелепипеда равны 8 и 2, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
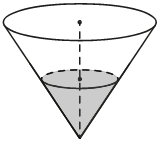 В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
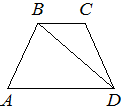 В трапеции ABCD известно, что AB=CD, ∠BDA=54° и ∠BDC=23°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD известно, что AB=CD, ∠BDA=54° и ∠BDC=23°. Найдите угол ABD. Ответ дайте в градусах.
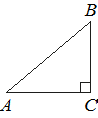 В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.

Комментарии: