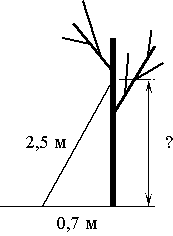
Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Лестница, дерево и земля представляют из себя прямоугольный треугольник. Высоту, на которой находится конец лестницы обозначим как X.
Тогда по теореме Пифагора мы можем записать 2,52=0,72+X2. Отсюда, X2=6,25-0,49, X2=5,76, X=2,4.
Ответ: высота равна 2,4 метра.
Поделитесь решением
Присоединяйтесь к нам...
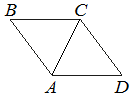В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
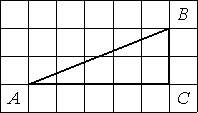Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
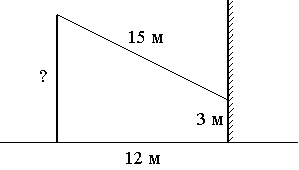От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
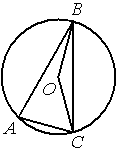Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: