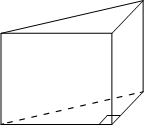
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
Объем прямой призмы равен произведению площади основания и высоты.
Высота известна, найдем площадь основания.
Площадь прямоугольного треугольника равна половине произведения катетов.
По теореме Пифагора найдем второй катет (обозначим его длину как x):
(√
34=9+x2
x2=34-9=25
x=5
Sоснования=3*5/2=15/2=7,5
V=7,5*6=45
Ответ: 45
Поделитесь решением
Присоединяйтесь к нам...
Какой наименьший угол (в градусах) образуют минутная
и часовая стрелки часов в 17:00?
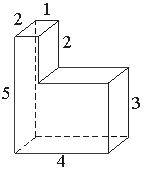Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
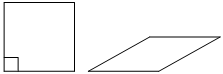Ромб и квадрат имеют равные стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 16.
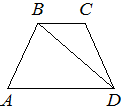В трапеции ABCD известно, что AB=CD, ∠BDA=40° и ∠BDC=30°. Найдите угол ABD. Ответ дайте в градусах.
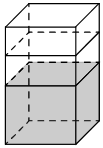В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды
в баке поднялся в 1,4 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре
1000 кубических сантиметров.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: