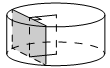
Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
В задаче не указано,
наклонный цилиндр или прямой. Но судя по рисунку - прямой.
Образующие прямого цилиндра перпендикулярны основаниям, следовательно, сечение - это
прямоугольник.
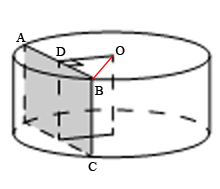Введем обозначения ключевых точек как показано на рисунке.
Вычислим длину хорды AB:
Рассмотрим треугольник ODB. Это
прямоугольный треугольник, так как OD перпендикулярен AB.
OB - это радиус основания.
По теореме Пифагора:
OB2=OD2+DB2
152=122+DB2
225=144+DB2
DB2=81
DB=9
AD=DB, так как OD -
серединный перпендикуряр по
второму свойству хорды.
Тогда AB=AD+DB=9+9=18
Площадь сечения равна произведению хорды и длины образующей:
S=AB*BC=18*14=252
Ответ: 252
Поделитесь решением
Присоединяйтесь к нам...
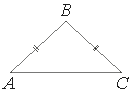В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
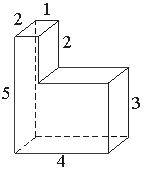Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
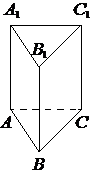Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
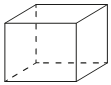Аквариум имеет форму прямоугольного параллелепипеда
с размерами 80 см x 30 см x 40 см. Сколько литров составляет объём аквариума?
В одном литре 1000 кубических сантиметров.
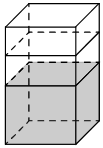В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды
в баке поднялся в 1,4 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре
1000 кубических сантиметров.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: