
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
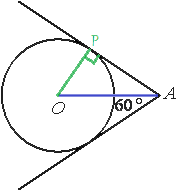 Проведем отрезок АО.
Проведем отрезок АО.
Обозначим одну из точек касания окружности и касательной как Р.
Проведем отрезок ОР.
ОР является радиусом и перпендикуляром к касательной АР (по свойству касательной).
Рассмотрим треугольник АОР.
Данный треугольник является прямоугольным,т.к. ОР перпендикулярен АР.
АО является биссектрисой угла, образованного касательными (свойство касательных прямых). Следовательно, угол РАО равен половине данного угла, т.е. 30°.
sinPAO=OP/AO (по определению синуса).
sin30°=8/AO
1/2=8/AO (по таблице синусов)
1=2*8/AO
AO=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
 Высота равностороннего треугольника равна 78√
Высота равностороннего треугольника равна 78√
Синус острого угла A треугольника ABC равен 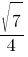 . Найдите CosA.
. Найдите CosA.
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
 Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.





Комментарии:
(2019-01-26 16:56:06) Администратор: Данила, я расписал решение немного подробней, надеюсь, стало понятней. Если нет, пишите.
(2019-01-25 16:13:14) Данила: И почему мы взяли именно значение синуса?
(2019-01-25 15:51:47) Данила: Откуда взято 2?
(2016-12-05 22:33:33) Администратор: катя, посмотрите задачу 101 из раздела "Статистика и теория вероятностей", очень похожа на Вашу.
(2016-12-05 17:26:10) катя: В среднем на 50 карманных фонариков, поступивших в продажу, приходится восемь неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен