
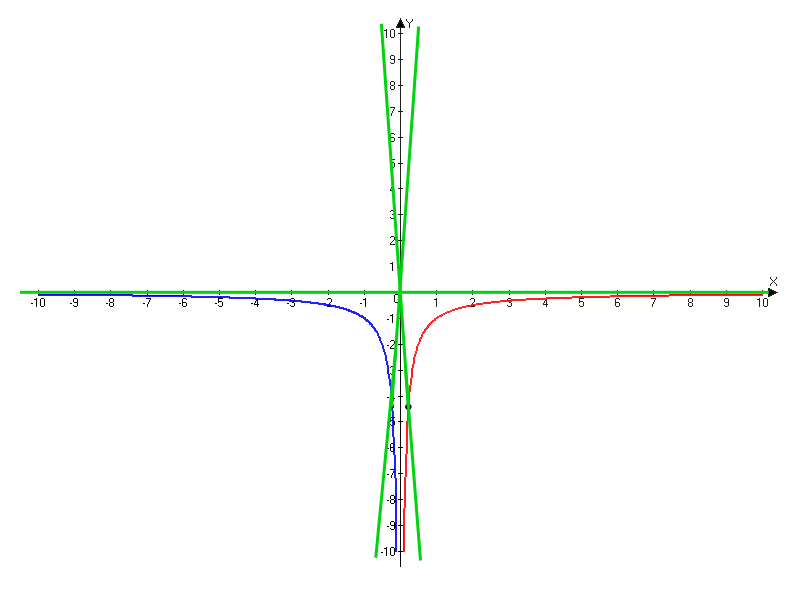
Постройте график функции 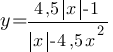 и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
Так как функция содержит модуль, то функцию надо разделить на две подфункции:
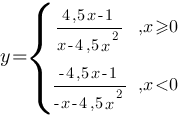
Рассмотрим первую подфункцию:
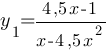 , при x≥0
, при x≥0
Область Допустимых Значений (ОДЗ).
Так как присутствует деление, то нужно исключить все x, при которых знаменатель будет равен нулю (так как деление на ноль не возможно).
x-4,5x2≠0
x(1-4,5x)≠0
x1≠0
1-4,5x≠0
1≠4,5x
10≠45x
2≠9x
x2≠2/9
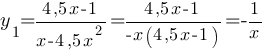 при x≥0
при x≥0
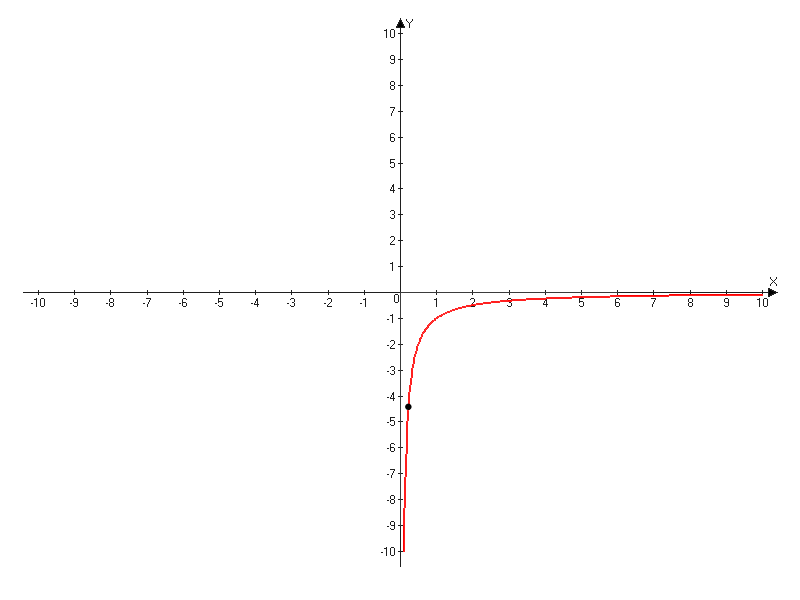
Построим график только для x≥0
| X | 1 | 2 | 4 | 5 |
| Y | -1 | -0,5 | -0,25 | -0,2 |
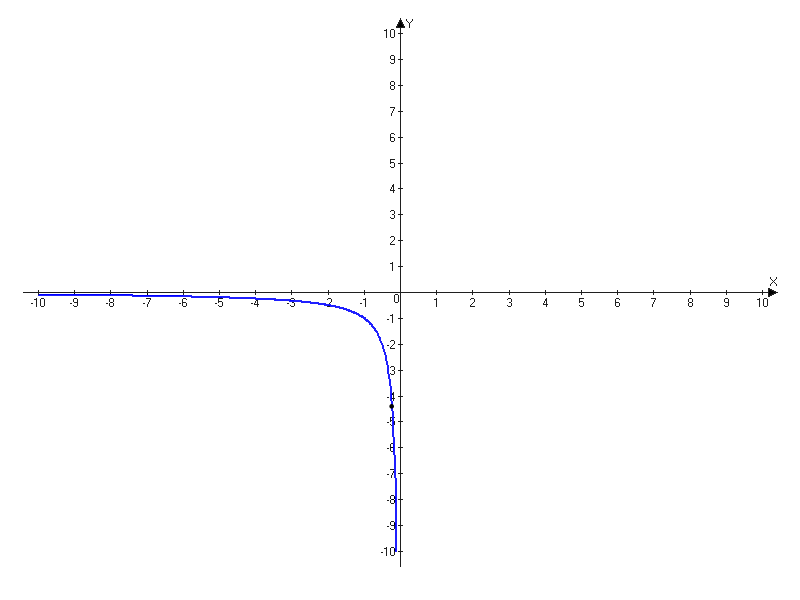
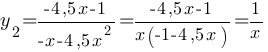 при x<0
при x<0| X | -1 | -2 | -4 | -5 |
| Y | -1 | -0,5 | -0,25 | -0,2 |
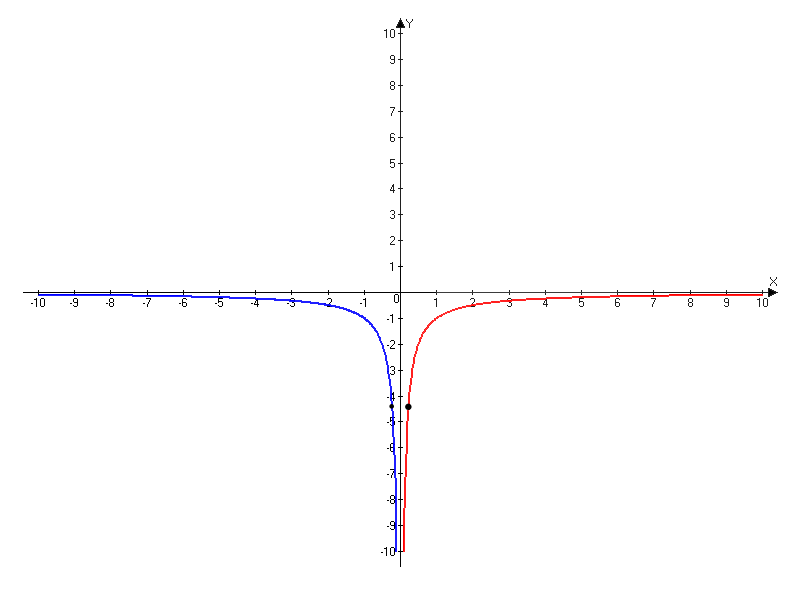
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения √
1) 28
2) 4√
3) 4
4) 16√
Постройте график функции y=4|x+6|-x2-11x-30 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Найдите значение выражения 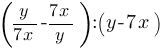 при x=1/7, y=1/5.
при x=1/7, y=1/5.
Какое из данных ниже чисел является значением выражения 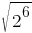 ?
?
1) 32
2) 16
3) 1/8
4) 8
Решите уравнение (2x-4)2(x-4)=(2x-4)(x-4)2.
Комментарии:
(2014-11-06 14:09:18) Администратор: Да, верно, в решении k=0 есть, а в ответе нет, исправлено! Спасибо!
(2014-11-06 14:05:57) : неверно еще к=0