Найдите p и постройте график функции y=x2+p, если известно, что прямая y=4x имеет с графиком ровно одну общую точку.
Две функции имеют точку пересечения, это означает, что графики обеих функций имеют общую точку. Следовательно, надо составить систему и решить ее:
y=x2+p
y=4x
4x=x2+p
x2-4x+p=0
Найдем корни этого квадратного уравнения:
D=(-4)2-4*1*p=16-4p
В условии сказано, что точка пересечения только одна, следовательно корень уравнения должен быть только один. Это условие выполняется, когда дискриминант равен нулю:
D=16-4p=0
p=4
x=-(-4)/(2*1)=2
y=4x=4*2=8
(2;8) - точка пересечения графиков.
Получаем функцию:
y=x2+4
График функции:
Поделитесь решением
Присоединяйтесь к нам...
Первый велосипедист выехал из посёлка по шоссе со скоростью 18 км/ч. Через час после него со скоростью 16 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 4 часа после этого догнал первого.
Поезд, двигаясь равномерно со скоростью 183 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 3 км/ч, за 13 секунд. Найдите длину поезда в метрах.
Решите систему неравенств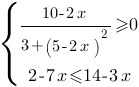 
Первые 5 часов автомобиль ехал со скоростью 55 км/ч, следующие 5 часов — со скоростью 75 км/ч, а последние 5 часов — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решите уравнение (x2-36)2+(x2+4x-12)2=0.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: