
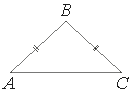
 В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
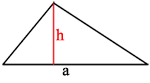
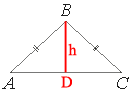 Проведем высоту к основанию треугольника.
Проведем высоту к основанию треугольника.
Так как h - высота, то треугольник ABD -
прямоугольный.
Тогда, по определению синуса:
sinA=BD/AB=3/5
BD=AB*3/5=25*3/5=5*3=15
Теперь воспользуемся теоремой Пифагора, чтобы найти AD.
AB2=BD2+AD2
252=152+AD2
625=225+AD2
AD2=625-225=400
AD=√400=20
По третьему свойству
равнобедренного треугольника,
высота является так же и
медианой, следовательно:
AC=2*AD=2*20=40
Зная основание и высоту треугольника можем найти его
площадь:
S=(1/2)AC*BD=(1/2)*40*15=20*15=300
Ответ: 300
Поделитесь решением
Присоединяйтесь к нам...
 В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
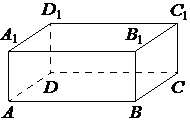 В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √
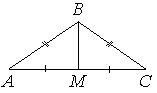 В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
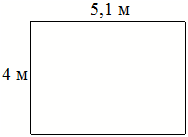 На плане указано, что прямоугольная комната имеет площадь 20,1 кв. м. Точные измерения показали, что ширина комнаты равна 4 м,
а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от площади, указанной на плане?
На плане указано, что прямоугольная комната имеет площадь 20,1 кв. м. Точные измерения показали, что ширина комнаты равна 4 м,
а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от площади, указанной на плане?
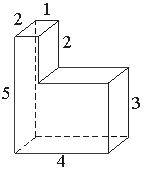 Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
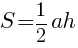


Комментарии:
(2021-02-01 17:06:11) Тимур: Найдите основание равнобедренного треугольника, если его боковая сторона равна 5, а косинус угла между боковыми сторонами равен 3/5