
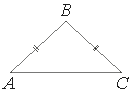
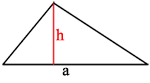
 В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB.
В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB.
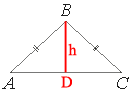 Проведем высоту к основанию треугольника.
Проведем высоту к основанию треугольника.
Площадь треугольника:
S=(1/2)AC*h
300=(1/2)40*h
300=(40/2)*h
300=20h
h=15=BD
Так как h - высота, то треугольник ABD -
прямоугольный.
Тогда мы можем воспользоваться
теоремой Пифагора:
AB2=BD2+AD2
Но нам неизвестна AD.
По третьему свойству
равнобедренного треугольника,
высота является так же и
медианой, следовательно:
AD=AC/2=40/2=20
Подставляем значения в теорему Пифагора:
AB2=152+202
AB2=225+400=625
AB=√625=25
Ответ: 25
Поделитесь решением
Присоединяйтесь к нам...
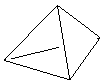 Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
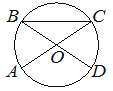 В окружности с центром O отрезки AC и BD — диаметры. Вписанный угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD — диаметры. Вписанный угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.
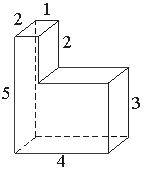 Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
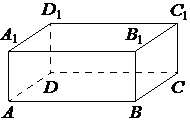 В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √
 В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB.
В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB.
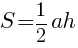


Комментарии: