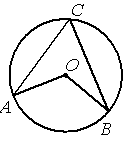
Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=65°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 65°*2=130°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=130°.
Ответ: /AOB=130°.
Поделитесь решением
Присоединяйтесь к нам...
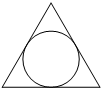Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
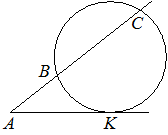Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
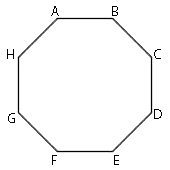ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: