
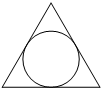
 Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
По
четвертому свойству равностороннего треугольника:
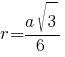
a√3=6r
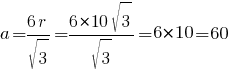
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
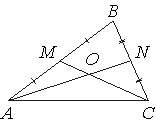 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
 В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 163°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 163°. Найдите угол C. Ответ дайте в градусах.
 В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
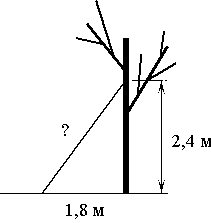 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
Комментарии:
(2024-03-10 22:53:07) настя : Радиус окружности, вписанной в равносто- ронний треугольник, равен 5 3 . Найдите длину стороны этого треуго