
 Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
AB=BC=CD=AD=DH+CH=24+2=26 (по
определению ромба).
Рассмотрим треугольник AHD.
AHD -
прямоугольный (т.к. AH -
высота), тогда по
теореме Пифагора:
AD2=AH2+DH2
262=AH2+242
676=AH2+576
AH2=676-576=100
AH=√100=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
 Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.
 Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
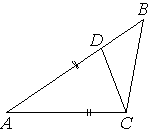 Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=19° и ∠ACB=160°. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=19° и ∠ACB=160°. Найдите угол DCB. Ответ дайте в градусах.
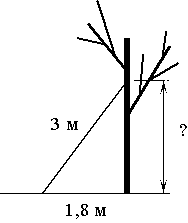 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Комментарии: