
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
 ∠GAE=∠BEA (т.к. они
накрест-лежащие)
∠GAE=∠BEA (т.к. они
накрест-лежащие)
∠GAE=∠BEA=∠BAE (т.к. AE -
биссектриса).
Получается, что треугольник ABE -
равнобедренный.
BF -
биссектриса, а по
свойству равнобедренного треугольника, она так же и
медиана и
высота.
Таким образом, получается, что треугольник ABF -
прямоугольный.
По
теореме Пифагора:
AB2=AF2+BF2
AB2=212+202
AB2=441+400=841
AB=√841=29
Ответ: 29
Поделитесь решением
Присоединяйтесь к нам...
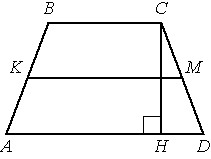 В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
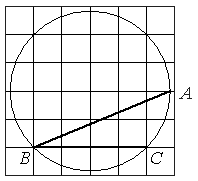 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
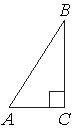 В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
 Длина хорды окружности равна 60, а расстояние от центра окружности до этой хорды равно 40. Найдите диаметр окружности.
Длина хорды окружности равна 60, а расстояние от центра окружности до этой хорды равно 40. Найдите диаметр окружности.
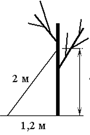 Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Комментарии: