
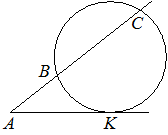
 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
По
теореме о касательной и секущей:
AK2=AB*AC
AK2=6*54=324
AK=√324=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
 Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 37°, угол ABC равен 25°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 37°, угол ABC равен 25°. Найдите угол ACB. Ответ дайте в градусах.
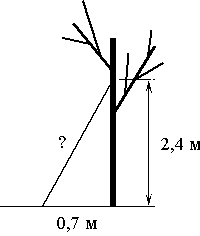 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м?
 Катеты прямоугольного треугольника равны 5√
Катеты прямоугольного треугольника равны 5√
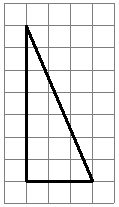 На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Комментарии: