
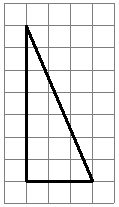
 На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Из
определения прямоугольного треугольника понятно, что катеты - это стороны прилегающие к прямому углу. В данной задаче катеты равны 7 и 3.
Очевидно, что 7 - длина большего катета.
Ответ: 7
Поделитесь решением
Присоединяйтесь к нам...
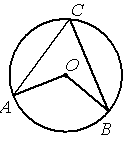 Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
 Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
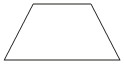 Один из углов равнобедренной трапеции равен 113°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Один из углов равнобедренной трапеции равен 113°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=177°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=177°. Найдите величину угла BOC. Ответ дайте в градусах.
 Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58. Найдите длину диагонали трапеции.
Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58. Найдите длину диагонали трапеции.
Комментарии: